方向余弦
方向余弦とは?
\(xyz\) 直交座標系で任意のベクトル \(\overrightarrow{v} = \langle v_1, v_2, v_3\rangle\) を考えます。
\(\overrightarrow{i}\)、\(\overrightarrow{j}\)、\(\overrightarrow{k}\) を基本ベクトルとして、\(\overrightarrow{v}\) と \(\overrightarrow{i}\) のなす角を \(\alpha\)、 \(\overrightarrow{v}\) と \(\overrightarrow{j}\) のなす角を \(\beta\)、 \(\overrightarrow{v}\) と \(\overrightarrow{k}\) のなす角を \(\gamma\) とします。
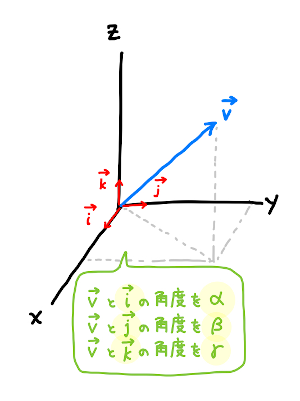
\(\alpha\)、\(\beta\)、\(\gamma\) はそれぞれ \(x\)軸、\(y\)軸、\(z\)軸との角度を表しています。これらを \(\overrightarrow{v}\) の direction angle (「方向角」と訳しておきます) といいます。
\(\overrightarrow{v}\) の始点を原点として、\(\overrightarrow{v}\) の終点とそこから \(x\)軸へ垂線を引きます。
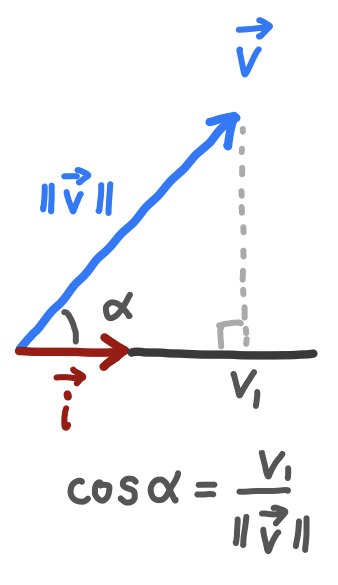
こうしてできる三角形から、\(\cos \alpha = \cfrac{v_1}{\| \overrightarrow{v}\|}\) がわかります。
\(y\)軸、\(z\) 軸についても同様に考えると、次の関係がわかります。
この \(\cos \alpha\)、\(\cos \beta\)、\(\cos \gamma\) を \(\overrightarrow{v}\) の方向余弦 (direction cosines) といいます。
内積の計算から方向余弦を考える
上では図からただちに、方向余弦の式を求めました。
ここでは内積の計算をすることで、同じ式が求められるか確かめてみましょう。
ベクトル \(\overrightarrow{v}\) は基本ベクトルを使って次のように書けます。
\[ \overrightarrow{v} = v_1 \overrightarrow{i} + v_2 \overrightarrow{j} + v_3 \overrightarrow{k} \]
\(\overrightarrow{i}\)、\(\overrightarrow{j}\)、\(\overrightarrow{k}\) はそれぞれ直交しているので、 \(\overrightarrow{i} \cdot \overrightarrow{j} = 0\)、\(\overrightarrow{i} \cdot \overrightarrow{k} = 0\) です。 よって、\(\overrightarrow{v}\) と \(\overrightarrow{i}\) との内積を考えると次のようになります。
また、\(\overrightarrow{v}\) と \(\overrightarrow{i}\) のなす角が \(\alpha\) であり、 \(\|\overrightarrow{i}\| = 1\) であることから、それらの内積は次のようにも書けます。
以上から、\(v_1 = \| \overrightarrow{v}\| \cos \alpha\) がわかりました。
したがって、 \(\cos \alpha = \cfrac{v_1}{\| \overrightarrow{v}\|}\) となります。
\(\overrightarrow{j}\)、\(\overrightarrow{k}\) についても同様です。
\(\overrightarrow{v}\) と同じ向きの単位ベクトルと方向余弦
さてここで、ベクトル \(\overrightarrow{v}\) 向きの単位ベクトルを考えます。
\(\overrightarrow{v}\) 向きの単位ベクトルは、\(\overrightarrow{v}\) 自身の長さ \(\| \overrightarrow{v} \|\) で割れば得られます。
\[ \frac{\overrightarrow{v}}{\|\overrightarrow{v}\|} = \frac{v_1}{\|\overrightarrow{v}\|} \overrightarrow{i} + \frac{v_2}{\|\overrightarrow{v}\|} \overrightarrow{j} + \frac{v_3}{\|\overrightarrow{v}\|} \overrightarrow{k} \]
上で見てきたように、これは方向余弦を使って次のようにかけます。
\[ \frac{\overrightarrow{v}}{\|\overrightarrow{v}\|} = \cos \alpha \overrightarrow{i} + \cos \beta \overrightarrow{j} + \cos \gamma \overrightarrow{k} \]
つまり \(\overrightarrow{v}\) の方向余弦とは「\(\overrightarrow{v}\) と同じ向きの単位ベクトルの成分」のことなのです。
方向余弦の問題
問題を解いて、理解を確かめてみましょう。
以上、方向余弦について説明しました。