部分積分
ここでは定積分を求めるための、部分積分 (integration by parts for definite integral) という積分方法について説明します。
「微分」のときは、少々複雑な関数でも「微分するにはこうする」という段取りが決まっています。ところが、積分については「こうすれば積分できる」という段取りが決まっていないので、 いろんなテクニックを駆使して積分していくしかありません。部分積分は「ややこしい式を簡単に積分するためのテクニック」のひとつです。
部分積分は \(f(x)\) と \(g(x)\) を \(x\) の関数として、次の関係のことを言います。
なんだかややこしそうですね。
でも、やりたいことは「簡単に積分する」ということなのです。
部分積分の成り立ち
被積分関数が \(x\) の関数である \(f(x)\) の導関数とします。すると、次のように定積分が計算できます (\(a\) と \(b\) は定数とします)。
\[ \int^b_a f'(x) dx = \Big[f(x)\Big]^b_a \]
これと全く同じ考えで、被積分関数が \(x\) の関数である \(f(x)\) と \(g(x)\) の積の導関数とします。すると、次のように定積分が計算できます。
\[ \int^b_a \{f(x)g(x)\}' dx = \Big[f(x)g(x)\Big]^b_a \]
ここで、微分の公式で \(\{f(x)g(x)\}' = f'(x)g(x) + f(x)g'(x)\) という関係があるので、上の式の左辺は次のように書き換えられます。
\[ \int^b_a \{f'(x)g(x) + f(x)g'(x)\} dx = \Big[f(x)g(x)\Big]^b_a \]
さらに左辺を書き換えて、式を整理すると直ちに次のようになります。
\[ \begin{aligned} \int^b_a f'(x)g(x) dx + \int^b_a f(x)g'(x) dx = \Big[f(x)g(x)\Big]^b_a \\ \therefore \ \ \int^b_a f(x)g'(x) dx = \Big[f(x)g(x)\Big]^b_a - \int^b_a f'(x)g(x) dx \end{aligned} \]
これで部分積分の式が出てきました。
部分積分とは?
さて、わざわざこんな形に式変形しましたが、一体どんな役に立つのでしょうか?
両辺の関係をよくみると、次のようなことがわかります。
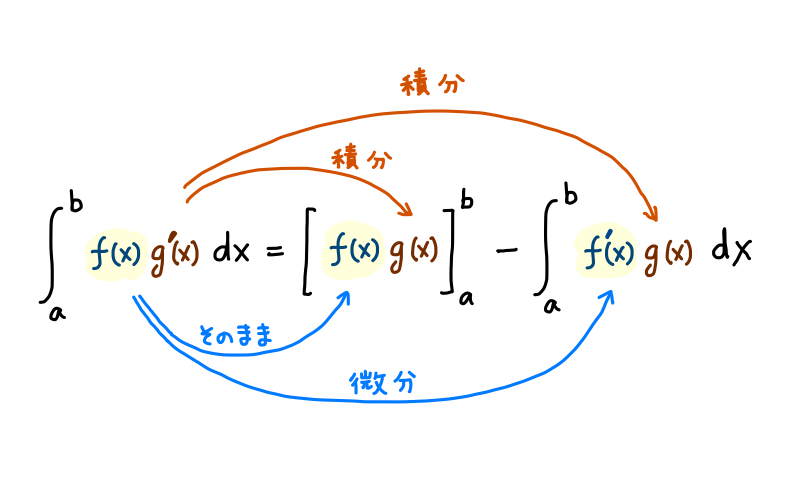
左辺の被積分関数に出てくる \(f(x)\) の部分だけ見ると、右辺に行っても積分されていません。 「そのまま」右辺に持ってきているところと、「微分して」右辺にもってきているところがあるだけです。
このため、ある関数を一度に積分するのは難しい場合でも、その関数を \(f(x)\) と \(g'(x)\) の掛け算で構成されているとみなして、 \(f(x)\) の部分と \(g(x)\) の部分をバラバラに考えることで、積分しやすくなる場合が出てくるのです。