微分可能でないことを直感的に理解する

「微分係数と導関数」では、\(f(x)\) の導関数 \(f'(x)\) を求めることを \(f(x)\) を微分するということを説明しました。 そして 導関数 \(f'(x)\) に特定の値を代入することで微分係数が求まり、微分係数は接線の傾きを表しているということも説明しました。

さて、それではいつでも微分できるか、というとそうではなくて、場合によっては微分できない時もあります。

導関数が接線の傾きの関数である、ということをふまえると、次の場合で微分できないことが直感的にわかります。

(1) \(x=x_0\) で関数 \(f(x)\) が連続でない場合。

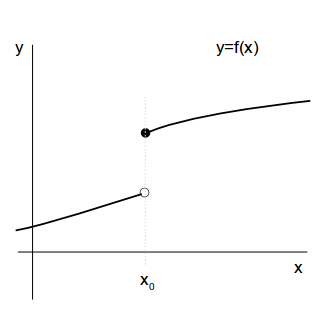
\(x=x_0\) でグラフがブツ切れているので、そこでは接線が考えられません。\(x=x_0\) で傾きが求まらない、つまり、\(x=x_0\) で微分不可能です。

(2) \(x=x_0\) でグラフが垂直になる場合。

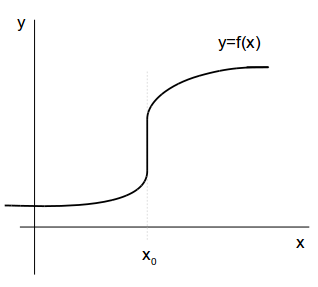
\(x=x_0\) で接線の傾きは無限大になる (発散する) ので導関数の定義に出てくる極限値が求まりません。すなわち微分できません。

(3) \(x=x_0\) でグラフが尖っている場合。

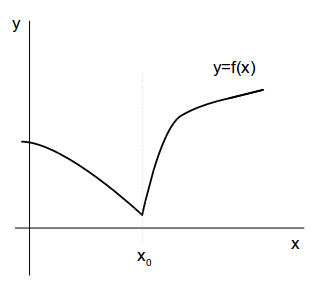
\(x=x_0\) でグラフが尖っているところでは、接線の傾きがひとつに定まりません。つまり、この場合 \(x=x_0\) で微分できません。

このように、\(x=x_0\) で微分可能かどうかは、グラフの様子がわかるときは直感的に直ちにわかります。