三角関数の合成公式

\(f(\theta) = a \cos \theta + b \sin \theta\) という関数がどんな値をとるか考えてみましょう。

\(\theta\) が変わると、\(\sin \theta\) や \(\cos \theta\) がそれぞれ大きくなったり小さくなったりします。このため、上の \(f(\theta)\) が \(\theta\) に対して、どのような値をとるかはすぐに分かりません。

そこで便利なのが、三角関数の合成公式と言われるものです。

三角関数の合成公式を使うと、上の \(f(\theta)\) は次のように書き直せます。

\[ \begin{aligned} f(\theta) &= a \cos \theta + b \sin \theta\\ &= A \sin( \theta + \alpha) \end{aligned} \]

ここで、\(A\) と \(\alpha\) は次を満たす値です。

\[ \begin{aligned} A &= \sqrt{a^2+b^2}\\ a &= A \sin \alpha \\ b &= A \cos \alpha \\ \end{aligned} \]

「公式」と言われるとつい考えるのをやめて、覚えてしまおうと思う人もいるかもしれません。丸暗記して覚えようと思っても忘れてしまったらアウトです。合成公式は意味がわかれば簡単なことなので、試験対策としても公式を導くことに慣れた方が良いです。

三角関数の合成公式を導く

\(f(\theta) = a \cos \theta + b \sin \theta\) を \(f(\theta) = A \sin( \theta + \alpha)\) という風に \(\cos\) を消して \(\sin\) だけの式に書き換えてみましょう。

まず、次のように \(xy\) 平面上に点 P をとります。

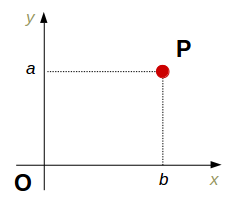
線分 OP を考えると、この長さは三角形 POb でピタゴラスの定理より \(\sqrt{a^2+b^2}\) になります。これを \(A\) とします。

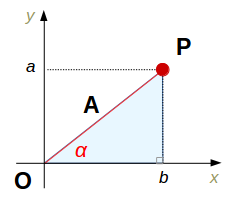
角\(\angle POb\) を \(\alpha\) とすると、 \(a = A \sin \alpha\) 、 \(b = A \cos \alpha \) となります。

すると、元の式は次のように変形できます。

\[ \begin{aligned} f(\theta) &= a \cos \theta + b \sin \theta \\ &= A \sin \alpha \cos \theta + A \cos \alpha \sin \theta\\ &= A (\sin \alpha \cos \theta + \cos \alpha \sin \theta)\\ &= A \sin( \alpha + \theta)\\ &= A \sin( \theta + \alpha) \end{aligned} \]

途中で \(\sin\) の加法定理を使っています。

三角関数の加法定理

\[ \begin{aligned} \sin (\alpha \pm \beta) &= \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos (\alpha \pm \beta) &= \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \end{aligned} \]

\(\sin\) については「サインコスプラコスサイン」、\(\cos\) は「コスコスマイナスサインサイン」です。

以上で、三角関数の合成公式が導けました。

上では合成公式として \(\sin\) にまとめる方法を示しましたが、\(\cos\) にすることもできます。点 P の座標を \(P(b, a)\) ではなく、\(P(a, b)\) ととるとわかりやすいと思います。