コーシーの積分定理

コーシーの積分定理 (Cauchy's Integral Theorem) について説明します。

はじめに、出てくる言葉のおさらいから始めます。

コーシー積分定理の「条件」に出てくること

「単連結な領域」というのは、次のような領域のことです。グルッと適当な丸を描いてできた領域です。

「丸」と書きましたが、別に尖っていてもよくて、ポイントは領域に「穴」が開いていないことです。下の図の領域は穴が開いているので、単連結ではありません。

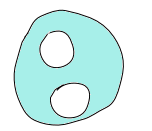
「単純閉曲線」というのは、次のようなシンプルな輪っかのことです。

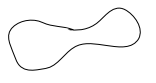
次のように交差している曲線は単純閉曲線ではありません。

ポイントは自己交差していないことです。

複素関数が「正則である」というのは「微分可能である」ということです。

正則なら「特異点がない」ということになります。特異点というのは、関数の分母をゼロにする極など、「正則ではない点」ということですから。

さて、上記の言葉の意味がはっきりわかっていれば、コーシーの積分定理で言っていることは簡単なことです。

\(f(z)\) が単連結な領域 \(D\) 上で正則な複素関数とします。\(C\) を \(D\) 内のある単純閉曲線であるとします。

つまり、下図のように特異点を含まない領域 \(D\) の中で、グルッと自己交差しない単純な輪っか \(C\) を考えています。

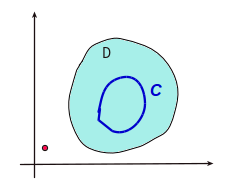
コッソリ描いた赤丸は特異点です。領域 \(D\) は特異点を避けています。

このときに、経路 \(C\) に沿った \(f(z)\) の線積分は常に \(0\) になる、というのがコーシーの積分定理です。

\[ \oint_{C} f(z) dz = 0 \]

複素関数の線積分は一般的には経路に依存します。しかし、今回の前提条件のように正則な領域 \(D\) で単純閉曲線 \(C\) を考えたら、グルッと線積分してくると \(0\) になるということです。