関数の連続性
関数の「極限」のおさらい
前のページでは関数の極限値について考えました。
簡単におさらいすると、「ある \(x=a\) で関数 \(f(x)\) が極限値 \(L\) を持つ」 ということは、「\(x\) のどちらの向きから \(a\) に近付いても同じ値 \(L\) に近付く」ということでしたね。
でも、極限値は \(x=a\) に「近付く」ということを考えていたのであって、 関数 \(f(x)\) が 「\(x=a\) そのもの」(つまり \(f(a)\) のこと) でどうなっているか、というのは考えていませんでした。 \(f(x)\) が \(x=a\) で定義されていなかったとしても、極限値が存在することはあるのです。
さて、極限がわかれば、連続性について勉強する準備はできました。
関数が連続であるとは
次の条件を満たすとき、関数 \(f(x)\) は点 \(x=a\) で連続であるといいます。
- \(f(a)\) が定義されている。
- \(\displaystyle{\lim_{x \to a} f(x)}\) が存在する。
- \(\displaystyle{\lim_{x \to a} f(x)} = f(a)\)
具体例で考えてみましょう。
次の関数は \(x=2\) で連続でしょうか?
\[ f(x) = \begin{cases} \ x + 1 & (x \not = 2) \\ \ 5 & (x = 2) \end{cases} \]
まず、\(f(2)\) が定義されているかどうかみてみると \(f(2)=5\) と定義されています。一つ目の条件はクリアです。
次に極限値 \(\displaystyle{\lim_{x \to 2} f(x)}\) が存在するかどうかですが、 下のグラフから右から \(x=2\) に近付いても、左から \(x=2\) に近付いても \(f(x)\) は \(3\) に近付いています。
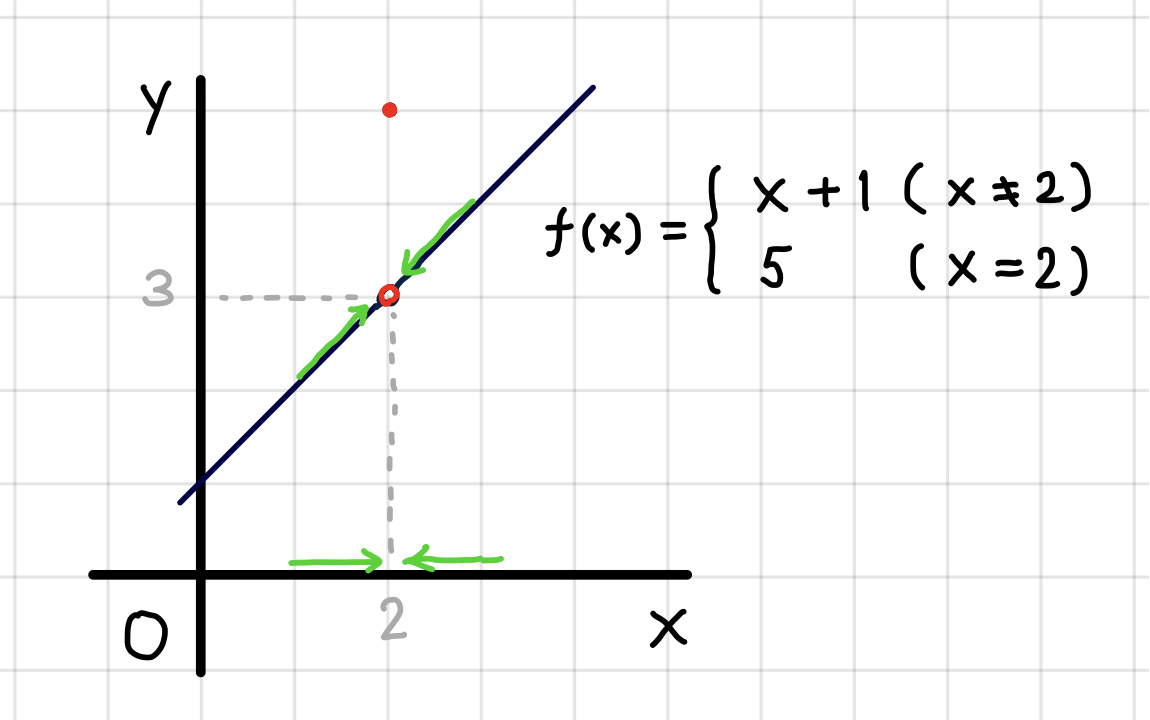
右側の極限値と左側の極限値が等しいので、極限値は存在して \(\displaystyle{\lim_{x \to 2} f(x) = 3}\) です。
これで、連続性の二つ目の条件もクリアです。
さて、最後の連続性の条件ですが、左辺は \(\displaystyle{\lim_{x \to 2} f(x) = 3}\)。 右辺は \(f(2) = 5\) ですから、\(\displaystyle{\lim_{x \to 2} f(x) \not = f(2)}\) です。
三つ目の条件をクリアできなかったので、この \(f(x)\) は \(x=2\) で連続ではない、ということになります。
グラフで言えば、\(x=2\) だけポツンとグラフが切れているので、普通の言葉でいうところの「連続」ではないだろうな、 というのはみればわかりますね。でも、数学でいうところの「連続性」というのはこのようなステップで考えるのです。
より正確にはε-δ 論法で考える必要があります。
関数の連続性の基本的な定理
「極限値の基本的な定理」でみたように、任意の多項式 \(f(x)\) は任意の実数 \(a\) に対して \(\displaystyle{\lim_{x \to a} f(x) = f(a)}\) でしたから、次は明らかです。
多項式は至る所で連続である。
次に連続な関数の四則演算について、次が成り立ちます。
\(D\) を定義域とする関数 \(f(x)\) と \(g(x)\) があり、\(D\) 内の点 \(x = a\) で \(f(x)\) も \(g(x)\) も連続ならば次が成り立つ。
- \(f(x) \pm g(x)\) は \(a\) で連続である。
- \(f(x)g(x)\) は \(a\) で連続である。
- \(f(x)/g(x)\) は \(a\) で連続である。(ただし \(D\) で \(g(x) \not = 0\) とする)
中間値の定理
\(f(x)\) が閉区間 \([a, b]\) で連続で \(f(a) \lt f(b)\) とする。 \(k\) を \(f(a) \lt k \lt (b)\) なる任意の値とする時、 \(f(c) = k\) とする \(c\) が \((a,b)\) に少なくとも一つ存在する。
下のグラフでは \((a, b)\) 内の\(3\)点 \(c_1, c_2, c_3\) で \(f(c_1) = k, f(c_2) = k, f(c_3) = k\) となっています。
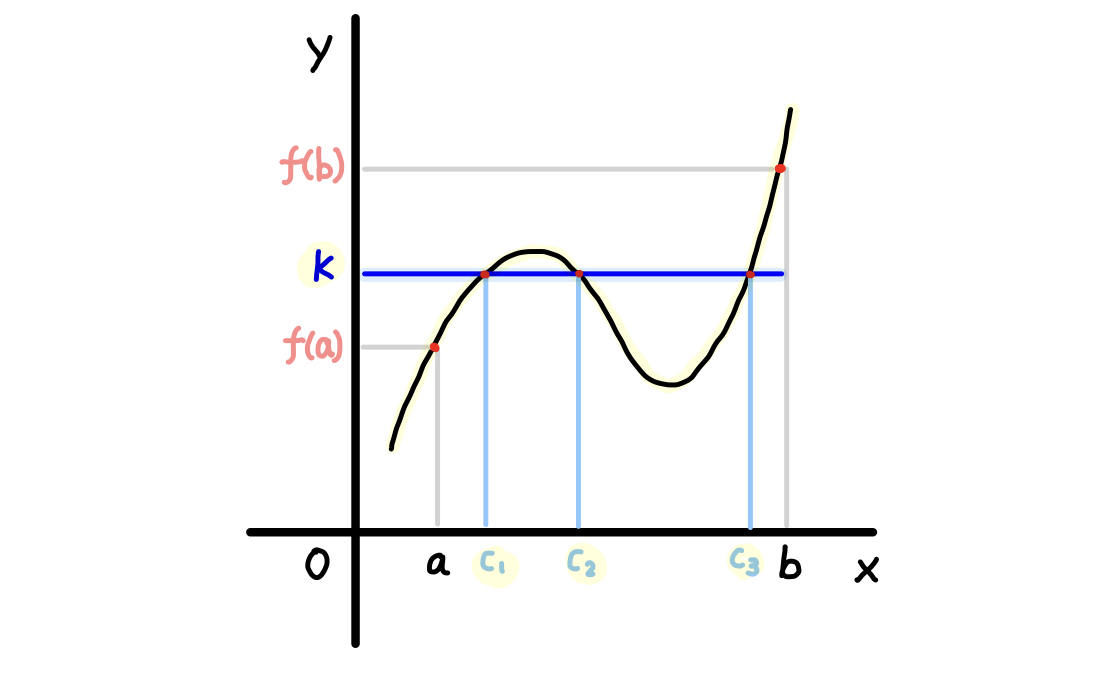
中間値の定理では開区間 \((a,b)\) に、このような点が存在することを述べています。