人口増加の微分方程式 (マルサスモデル)

ここでは、各国の人口増加率を元に、人口がどのように増加していくか計算してみましょう。

人口増加率とは？

アメリカやカナダでは現在、人口増加率は 0.96% と言われています。

人口増加率が 0.96% ということは人口 100 人いたら、単位時間 (この場合 1 年) で \(100 * 0.0096 = 0.96\) から \(0.96\)人増えるということです。つまり、1年経ったら \(100.96\) 人になっているということですね。そして、もう一年経ったら今度は \(100.96 * 0.0096 \approx 0.97\) 人増えることになります。

最初の 1 年は \(0.96\) 人増えていますが、次の 1 年では \(0.97\) 人増えています。

増加量は増加していく数に増加率をかけて計算するので、増加「率」が一定でも毎年同じ数が増えるわけではなく、増加「量」はどんどん増えていく、ところがポイントです。

変化から式を作る

さて、さっそく人口を表す式がどうなるか考えてみましょう。

今分かっているのは、次の関係です。

(単位時間での人口増加量) = (人口増加率) \(\times\) (人口)

今、人口 \(y\) を時間 \(t\) の関数として \(y = y(t)\)、人口増加率を \(k\) と書くと、上の関係は次のように書けます。

\[ \frac{dy}{dt} = ky \]

このように変化率などを元に数式を立てると、自然と微分方程式がでてきます。

これを解いて \(y\) がわかれば、人口の時間変化がわかります。カナダの人口は 2017年で約 3700 万人だそうですので、これを \(t = 0\) のときの値 (初期値 \(y_0\)) として、上の微分方程式を解いてみましょう。

増加率一定の時の微分方程式を解く

\[ \frac{dy}{dt} = ky \]

この微分方程式は、変数分離形なので次のように式変形できます。

変数分離形の微分方程式については、次のページをみてください。
変数分離形の微分方程式の解き方

\[ \begin{aligned} \frac{dy}{dt} &= ky \\ \int \frac{dy}{y} &= \int k dt\\ \ln |y| &= kt + C\\ |y| &= e^{kt+C}\\ y &= \pm e^{kt+C} \\ \therefore \ y &= A e^{kt} \end{aligned} \]

ここで \(A = \pm e^C\) としています。上で \(C\) は任意の定数なので、\(A\) も同じく任意の定数です。特に上の式では \(t = 0\) としたときに、\(y(0) = A \cdot e^{0} = A \) となるので、\(A\) は \(y\) の \(t=0\) のときの初期値 \(y_0\) になります。

よって、\(A\) を \(y_0\) と書き直すと、人口増加率 \(k\) が一定のときの、人口 \(y\) の時間変化を表す式として、次の関係式が求まりました。

\[ y(t) = y_0 e^{kt} \]

具体的にカナダの場合は \(k = 0.0096\)、\(y_0 = 3600\) ですから、人口の時間変化は次のように表されることがわかりました。

\[ y(t) = 3600 e^{0.0096t} \]

グラフを書くと次のようになります。

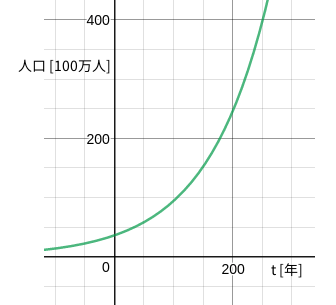
ここでみたように、人口の増加率が人口そのものに比例するとして、数式を立てて考える考え方は、 18 世紀のイギリスの経済学者であるトマス・ロバート・マルサスがはじめて示したとされ、マルサスモデル と呼ばれます。

「人口は必ずマルサスモデルに従って増える」ということではありません。マルサスモデルは「『人口の増加率が人口そのものに比例する』と考えるならば、この式に従う」ということを示すものです。現象を数学の言葉で表したものを、一般に数理モデルといいますが、マルサスモデルは数理モデルの一つです。

マルサスモデルの倍加時間

人口が \(t=0\) のときの倍、すなわち \(y = 2y_0\) になる時間 \(t\) を、倍加時間 (doubling time) といいます。人口増加がマルサスモデルに従うとしたときの、倍加時間を求めてみましょう。

上の式で \(y=2y_0\) としたときの \(t\) が倍加時間なので、次のように計算できます。

\[ \begin{aligned} 2y_0 &= y_0 e^{kt}\\ 2 &= e^{kt} \\ kt &= \ln 2 \\ \therefore \ t &= \frac{1}{k} \ln 2 \end{aligned} \]

従って、\(k = 0.0096\) のときの倍加時間は \(t = \ln 2 / 0.0096 \approx 72.2\) となります。つまり、カナダの人口増加がもし、マルサスモデルに順うのであれば、\(72.2\) 年後には、2017年の人口の倍である 7200万人になります。

70年後には2倍以上？

ちなみに 2018年11月現在、ウィキペディアのエントリーで「人口増加率は、一年間に人口が1%ずつ増加する国は、70年後には人口が2倍以上になり」と記載されています。その根拠はこの倍加時間の計算によるものです。

増加率が 1%、つまり \(k=0.01\) のとき、倍加時間は \(\ln 2 / 0.01 \approx 69.3\) であり、70 年弱で 2 倍になります。

マルサスモデルでは時間が経つにつれて無制限に人口増加が起きることになり、特に \(t\) が大きい所では、人口が無限大になり現実的な解でないことは明らかです。

これはマルサスモデルが、増加率を「常に一定」としていることから起きています。増加率をうまいこと調整した数理モデルに、ロジスティックモデルなどがあります。ロジスティックモデルについては、次のページを参考にしてください。

ロジスティック方程式とは

以上、マルサスモデルについて説明しました。