曲面 \(z=g(x,y)\) の法線

ここでは以前の記事「面積素とパラメータ (曲面 z=g(x,y) の場合)」に引き続き、 \(xyz\) 直交座標系で

\[ z=g(x,y) \]

で表される曲面 \(S\) を考えます。

面積素

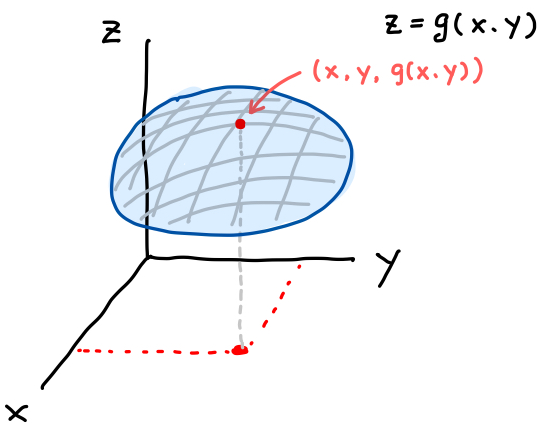
この曲面 \(S\) は、\(S\) 上で微分可能であるために、滑らかな曲面を考えます。

この曲面上の点の位置ベクトルは

\[ \overrightarrow{r} = x \overrightarrow{i} + y \overrightarrow{j} + g(x,y) \overrightarrow{k} \]

です。成分表示で書けば \(\overrightarrow{r} = \langle x, y, g(x,y) \rangle\) です。

さて、この曲面上のある点 \(P\) を \(\overrightarrow{r} = \langle x, y, g(x,y) \rangle\) とします。

点 \(P\) から \(x\) 方向に微小量 \(\Delta x\) だけ動いた点を点 \(Q\)、点 \(P\) から \(y\) 方向に微小量 \(\Delta y\) だけ動いた点を点 \(S\) とします。

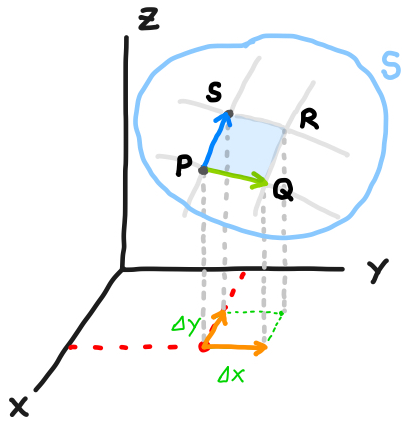
曲面上の点

すると、点 \(Q\)、点 \(S\) はそれぞれ、次のように書けます。

\[ \begin{aligned} \text{\small{点}}Q&: \overrightarrow{r}(x+\Delta x, y) &= \overrightarrow{r}(x,y) + \frac{\partial \overrightarrow{r}}{\partial x} \Delta x\\ \text{\small{点}}S&: \overrightarrow{r}(x, y+\Delta y) &= \overrightarrow{r}(x,y) + \frac{\partial \overrightarrow{r}}{\partial y} \Delta y \end{aligned} \]

つまり点 \(P\) を基準として、点 \(Q\)、点 \(S\) はそれぞれ、\(\displaystyle\frac{\partial \overrightarrow{r}}{\partial x} \Delta x\)、 \(\displaystyle\frac{\partial \overrightarrow{r}}{\partial y} \Delta y\)　だけ移動した点にあります。

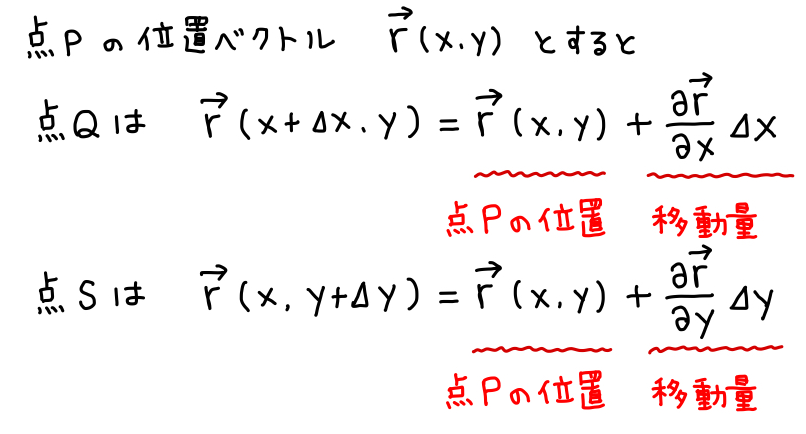
曲面上の点

これでベクトル \(\overrightarrow{PQ}\) の向きは \(\displaystyle\frac{\partial \overrightarrow{r}}{\partial x}\) で、ベクトル \(\overrightarrow{PS}\) の向きは \(\displaystyle\frac{\partial \overrightarrow{r}}{\partial y}\) であることがわかりました。

法線は \(\overrightarrow{PQ}\) と \(\overrightarrow{PS}\) 両方に垂直な向きは法線方向になります。

面積素

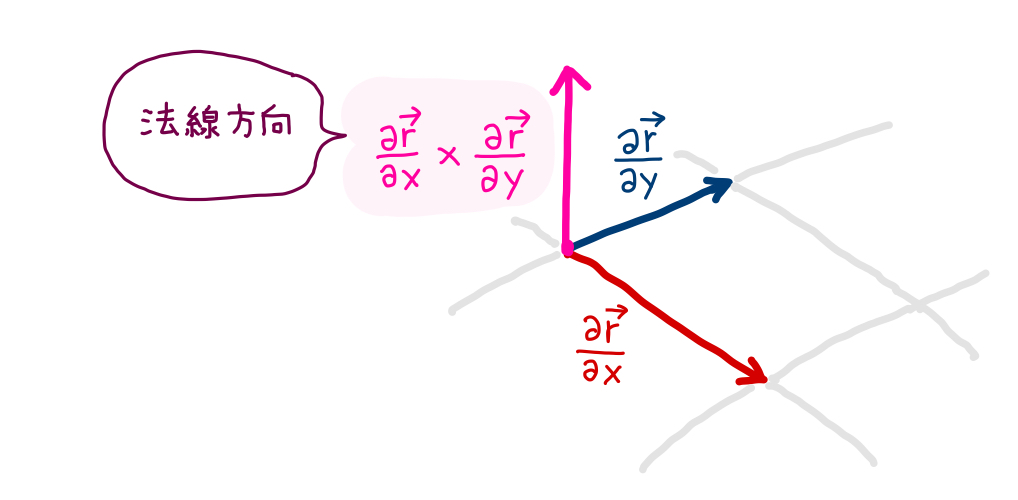
従って

\[ \frac{\partial \overrightarrow{r}}{\partial x} \times \frac{\partial \overrightarrow{r}}{\partial y} \]

は法線方向を向きます。

大きさを 1 にするために、そのベクトルの大きさそのもので割ると、単位法線ベクトル \(\overrightarrow{n}\) がわかります。

\[ \overrightarrow{n} = \frac{\cfrac{\partial \overrightarrow{r}}{\partial x} \times \cfrac{\partial \overrightarrow{r}}{\partial y}}{\Big\| \cfrac{\partial \overrightarrow{r}}{\partial x} \times \cfrac{\partial \overrightarrow{r}}{\partial y} \Big\|} \]

ここで、

\[ \overrightarrow{r} = x \overrightarrow{i} + y \overrightarrow{j} + g(x,y) \overrightarrow{k} \]

であることを思い出すと、もう少し式変形が進められます。

\(\overrightarrow{r}\) を \(x\) や \(y\) で偏微分したベクトルは、成分をそれぞれ \(x\) や \(y\) で偏微分することでもとまるので、次のようになります。

\[ \begin{aligned} \frac{\partial \overrightarrow{r}}{\partial x} &= \overrightarrow{i} + \frac{\partial g}{\partial x} \overrightarrow{k}\\ \frac{\partial \overrightarrow{r}}{\partial y} &= \overrightarrow{j} + \frac{\partial g}{\partial y} \overrightarrow{k}\\ \end{aligned} \]

これらのベクトル積は次のように計算できます。

\[ \begin{aligned} \frac{\partial \overrightarrow{r}}{\partial x} \times \frac{\partial \overrightarrow{r}}{\partial y} &= \begin{vmatrix} \overrightarrow{i} && \overrightarrow{j} && \overrightarrow{k}\\ 1 && 0 && \cfrac{\partial g}{\partial x}\\ 0 && 1 && \cfrac{\partial g}{\partial y} \end{vmatrix}\\ &= - \frac{\partial g}{\partial x} \overrightarrow{i} - \frac{\partial g}{\partial y} \overrightarrow{j} + \overrightarrow{k} \end{aligned} \]

このベクトルの大きさは、成分を二乗して足し合わせたものの平方根で、次のようにかけます。

\[ \Big| \frac{\partial \overrightarrow{r}}{\partial x} \times \frac{\partial \overrightarrow{r}}{\partial y} \Big| = \sqrt{\Big(\cfrac{\partial g}{\partial x}\Big)^2 + \Big(\cfrac{\partial g}{\partial y}\Big)^2 + 1} \]

上で得られた結果を代入すると、曲面 \(S (z=g(x,y))\) の単位法線ベクトル \(\overrightarrow{n}\) は次の式になることがわかります。

\[ \overrightarrow{n} = \frac{- \cfrac{\partial g}{\partial x} \overrightarrow{i} - \cfrac{\partial g}{\partial y} \overrightarrow{j} + \overrightarrow{k}}{\sqrt{\Big(\cfrac{\partial g}{\partial x}\Big)^2 + \Big(\cfrac{\partial g}{\partial y}\Big)^2 + 1}} \]

この式はしばしば \(p\) と \(q\) を使って次のように書かれます。

曲面 \(z=g(x,y)\) の単位法線ベクトルは \(p = \displaystyle\cfrac{\partial g}{\partial x}\)、\(q = \displaystyle\cfrac{\partial g}{\partial y}\) として

\[ \overrightarrow{n} = \frac{- p \overrightarrow{i} - q \overrightarrow{j} + \overrightarrow{k}}{\sqrt{p^2 + q^2 + 1}} \]

最初はあまり簡単になったように見えないかもしれませんが、実際に問題を解いて使ってみると、とても簡単に使えることがわかると思います。