重積分の変数変換
ここでは重積分における、変数変換方法の直感的なイメージについて説明します。特に二変数関数の重積分 (二重積分) と三変数関数の重積分 (三重積分) について考えます。
重積分とは
変数 \(x\) と \(y\) の関数 \(f(x,y)\) を考えます。 関数 \(f(x,y)\) の領域 \(R\) での重積分というのは次のようなものです。
領域 \(R\) を \(n\) 個の面積要素に分けます。\(k\) 番目の面積要素を \(\Delta A_k\) と書きます。 また、\(\Delta A_k\) 内の点 \(P_k\) を \(P_k(x_k, y_k)\) とします。\(P_k\) での関数値は \(f(x_k, y_k)\) です。
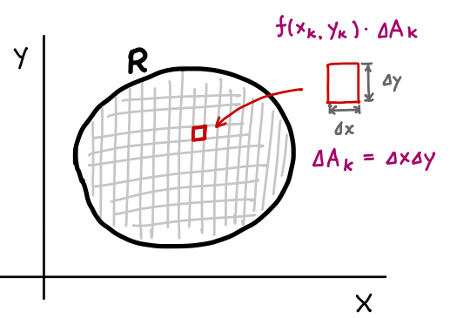
このとき、次の式のように \(P_k\) での関数値と面積要素の関の和を考えます。
\[ \sum_{k=1}^{n} f(x_k, y_k) \Delta A_k \]
ここで \(n\) を無限大にしたとき、つまり \(R\) を無限に分割したときの極限値が二重積分になります。
\[ \iint_R f(x,y) dA = \lim_{n \to \infty} \sum_{k=1}^{n} f(x_k, y_k) \Delta A_k \]
\(\Delta A\) は、\(x\) と \(y\) で書けば \(\Delta A = \Delta x \Delta y\) ですから、\(dA\) も \(dA = dx dy\) と書き下せます。
極座標のときの重積分
領域 \(R\) が円の時などは、\(x\) と \(y\) の直交座標で考えるより、\(\rho\) と \(\theta\) の極座標を考えて、\(x = \rho \cos \theta\)、\(y = \rho \sin \theta\) とした方が、 計算が簡単になる場合が多いです。
\(\rho\) はギリシャ文字のローです。極座標で原点からの距離を表すのに、よく使われます。
このとき、面積要素は下図で、薄ピンク色の部分がほぼ長方形とみなすことで、縦横、\(\Delta \rho\)、\( \rho \Delta \theta\) の掛け算として \(\Delta S = \rho \Delta \theta \Delta \rho\) となります。
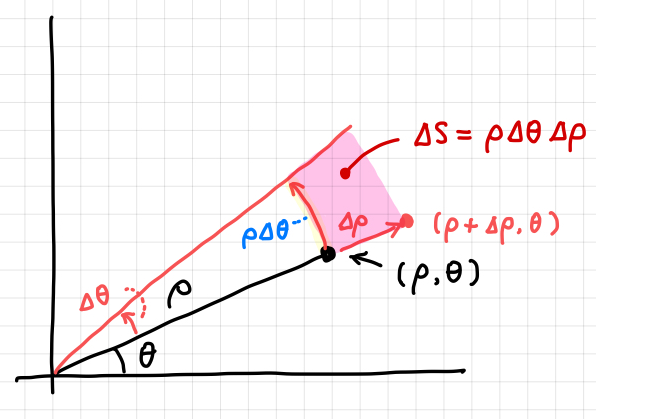
つまりこの時の重積分は変数を \(x, y\) から \(\rho, \theta\) に替えるには次のようにすれば良いことになります。
\[ \iint_R f(x,y) dS = \iint_D f(x(\rho,\theta),y(\rho,\theta)) \rho d\rho d\theta \]
ここで領域 \(D\) は変数変換後の \(r\) と \(\theta\) の定義域です。
\(x\) と \(y\) を \(u\) と \(v\) で表したときの変数変換
さて、それでは一般的に \(x, y\) がパラメータ \(u, v\) で記述されているときのことを考えてみましょう。 \(x = g(u, v)\)、\(y=h(u, v)\) と記述される場合です。
上の場合でいえば \(u\) を \(\rho\)、\(v\) を \(\theta\) とすれば、 \(g(\rho,\theta) = \rho \cos \theta\)、\(h(\rho, \theta)= \rho \sin \theta\) ということですね。
さてこのとき、点\(A(x(u_0, v_0), y(u_0, v_0))\) から、\(u\)、\(v\) がそれぞれ \(\Delta u\)、\(\Delta v\) だけ増加した時の点を考えます。
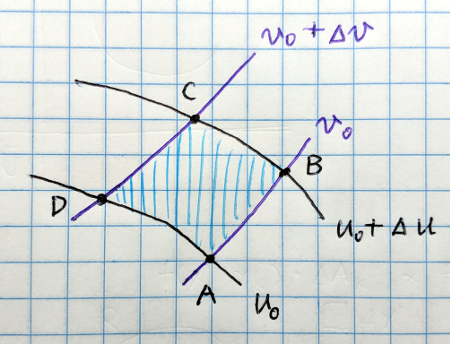
それぞれの座標は次のようになります。
\[ \begin{aligned} &A (x(u_0, v_0), \ y(u_0, v_0)) \\ &B ( x(u_0 + \Delta u, v_0), \ y(u_0 + \Delta u, v_0) ) \\ &\approx ( x(u_0,v_0) + \displaystyle\frac{\partial x}{\partial u} \Delta u, \ y(u_0,v_0) + \displaystyle\frac{\partial y}{\partial u} \Delta u) \\ &C(x(u_0 + \Delta u, v_0 + \Delta v), \ y(u_0 + \Delta u, v_0 + \Delta v) \\ &\approx \cdots \\ &D(x(u_0, v_0+\Delta v), \ y(u_0, v_0+\Delta v) \\ &\approx (x(u_0,v_0)+\frac{\partial x}{\partial v} \Delta v, \ y(u_0,v_0)+\frac{\partial y}{\partial v} \Delta v)\\ \end{aligned} \]
面積要素は \(\overrightarrow{AB}\) と \(\overrightarrow{AD}\) が作る平行四辺形の面積になります。
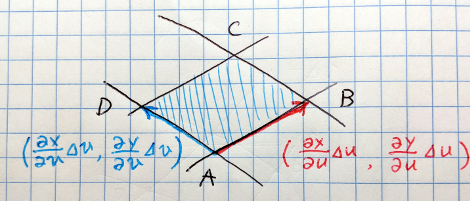
上に示した座標から、それぞれのベクトルは次のように書けます。
\[ \begin{aligned} \overrightarrow{AB} &= \Bigg[ \frac{\partial x}{\partial u} \Delta u, \ \frac{\partial y}{\partial u} \Delta u \Bigg]\\ \overrightarrow{AD} &= \Bigg[ \frac{\partial x}{\partial v} \Delta v, \ \frac{\partial y}{\partial v} \Delta v \Bigg]\\ \end{aligned} \]
二つのベクトルが作る平行四辺形の面積は、それらのベクトル積の大きさに等しい ので、 面積要素は次のようになります。
\[ \begin{aligned} \Delta A &= \| \overrightarrow{AB} \times \overrightarrow{AD} \| \\ &= \Bigg\| \Bigg(\frac{\partial x}{\partial u} \Delta u \frac{\partial y}{\partial v} \Delta v - \frac{\partial x}{\partial v} \Delta v \frac{\partial y}{\partial u} \Delta u\Bigg) \overrightarrow{k} \Bigg\| \\ &= \Bigg| \frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u} \Bigg| \Delta u \Delta v \\ \end{aligned} \]
これで面積要素 \(\Delta A =\Delta x \Delta y\) を \(u\) と \(v\) を使って書き換えることができました。
よって、上の重積分は次のように書き換えられます。
\[ \iint_R f(x,y) dA = \iint_D f(x(u, v),y(u,v)) \Bigg| \frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u} \Bigg| dudv \]
尚、次のように定義される行列式 \(J\) をヤコビアンといいます。
\[ J(u,v) = \frac{\partial (x, y)}{\partial (u, v)} = \begin{vmatrix} \cfrac{\partial x}{\partial u} & \cfrac{\partial x}{\partial v}\\ \cfrac{\partial y}{\partial u} & \cfrac{\partial y}{\partial v} \end{vmatrix} = \frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u} \]
上の面積要素の計算で出てきた、\(\Delta A\) と \(\Delta u \Delta v\) の比率を表す部分は、ヤコビアンの絶対値になります。 ヤコビアンを使って書き直すと、次のように書けます。
\[ \iint_R f(x,y) dA = \iint_D f(x(u, v),y(u,v)) \Bigg| \frac{\partial (x, y)}{\partial (u, v)} \Bigg| dudv \]
\(x = \rho \cos \theta\)、\(y = \rho \sin \theta\) のとき、ヤコビアン \(J(\rho,\theta)\) を求めよ
問題の変数変換は極座標変換です。
\[ \begin{aligned} &\frac{\partial x}{\partial \rho} \frac{\partial y}{\partial \theta} - \frac{\partial x}{\partial \theta} \frac{\partial y}{\partial \rho} \\ &= \cos \theta \cdot \rho \cos \theta - (-\rho \sin \theta) \cdot \sin \theta\\ &= \rho ( \cos^2 \theta + \sin^2 \theta ) \\ &= \rho \end{aligned} \]
したがって、面積要素は \(dA = dx dy = \rho d\rho d\theta\) となることがわかります。