三角不等式の証明
三角不等式 (triangle inequality) というのは次の式です。
\[
|a + b| \le |a| + |b|
\]
証明にはいろいろな方法がありますが、ここでは三角不等式の簡単な証明方法を紹介します。
まず、実数 \(x\) の絶対値は、定義から次の通りです。
\[
|x| = \begin{cases}
x &( x \ge 0)\\
-x &( x \lt 0)
\end{cases}
\]
よって \(x \ge 0\) のとき \( x \le |x|\) 、\(x \lt 0\) のとき \(-x \le |x|\) です。
\(a + b \ge 0\) のとき、
\[
|a + b| = a + b \le |a| + |b|
\]
が成り立つ。
また \(a + b \lt 0\) のとき、
\[
|a + b| = -(a + b) = (-a) + (-b) \le |a| + |b|
\]
となり成り立つ。
以上で全ての実数 \(a\)、\(b\) に対し、題意の不等式が成り立ちます。
幾何学的にみておくと
ベクトル \(\overrightarrow{a}\) 、 \(\overrightarrow{b}\) とその和 \(\overrightarrow{a} + \overrightarrow{b}\) がなす三角形を考えます。
ベクトルをまだ学習していない、という人はベクトルを「矢印のついた線分」と読み替えてください。
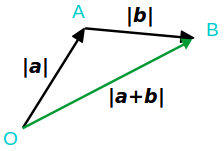
すると、ベクトルの大きさ (絶対値) の関係から、幾何学的に \(|a+b| \le |a| + |b|\) が成り立ちます。
\(\overrightarrow{a} + \overrightarrow{b}\) の始点 O から終点 B に行くときに、\(\overrightarrow{a} + \overrightarrow{b}\) のように直線 OB ルートで行く距離よりも、A を経由する \(\overrightarrow{a}\) 、 \(\overrightarrow{b}\) の個別ルートを移動する方が道のりが長くなるということです。