単位行列と基本行列

単位行列

\(n\) 次の正方行列で、対角成分が全て \(1\) で、他の成分が \(0\) の行列を、 単位行列 (identity matrix) といいます。 \(n\)次の単位行列は通常、\(I_n\) で表されます。

日本の教科書では単位行列を \(E\) で表す場合も多いです。しかし、このサイトでは、後述の基本行列を \(E\) で表し、単位行列は \(I\) で記載することにします。

例えば、\(2\)次の単位行列 \(I_2\) は

\[ I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]

であり、\(3\) 次の単位行列 \(I_3\) は

\[ I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

です。

任意の \(m\) 行 \(n\) 列の行列 \(A\) と単位行列の積は \(A\) になります。

\[ \begin{aligned} I_m A &= A\\ A I_n &= A \end{aligned} \]

正方行列 \(A\) に一度の基本変形を施すことで、単位行列が得られるとき、その行列 \(A\) を 基本行列 (elementary matrix) といいます。

単位行列に、ひとつの基本変形を施して得られる行列が基本行列であるともいえます。

正方行列 \(A\) に基本行列を左からかけることは、\(A\) に行列の行基本変形を行うことを意味します。また、行列 \(A\) に基本行列を右からかけることは、\(A\) に行列の列基本変形を行うことを意味します。

基本行列は、後述のように対応する基本変形毎に \(P\)、\(Q\)、\(R\) などの記号が使われます。または、基本行列を全てひっくるめて、記号 \(E\) で表します。

具体例は「行列の基本変形」でみたので、ここでは使われる記号を整理しておきます。

行列 \(A\) の「\(i\) 行目と \(j\) 行目を入れ替える」基本変形では、次の基本行列 \(P_n(i,j)\) を、\(A\) の左からかけます。

行列 \(A\) の「\(i\) 列目と \(j\) 列目を入れ替える」基本変形では、次の基本行列 \(P_n(i,j)\) を、\(A\) の右からかけます。

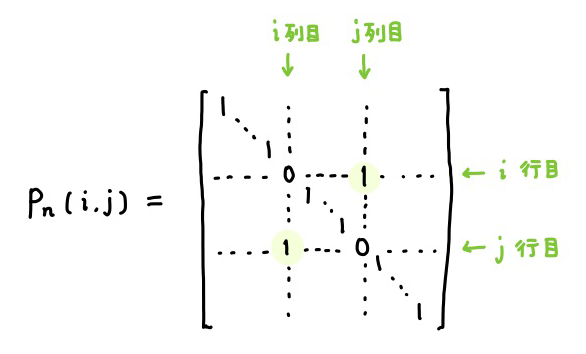
行列の成分が書いていないところは、全て \(0\) です (下記の \(Q\)、\(R\) も同様)。

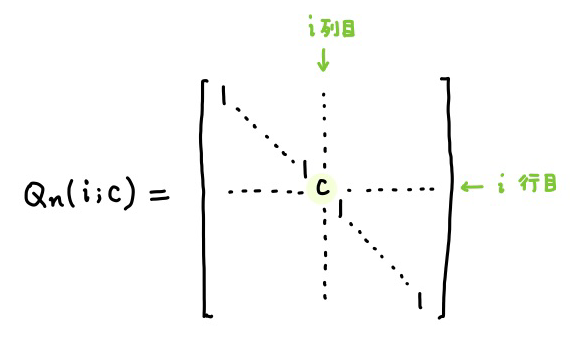
行列 \(A\) の「\(i\) 行目を \(c\) 倍する」基本変形では、次の基本行列 \(Q_n(i;c)\) を、\(A\) の左からかけます。

行列 \(A\) の「\(i\) 列目を \(c\) 倍する」基本変形では、次の基本行列 \(Q_n(i;c)\) を、\(A\) の右からかけます。

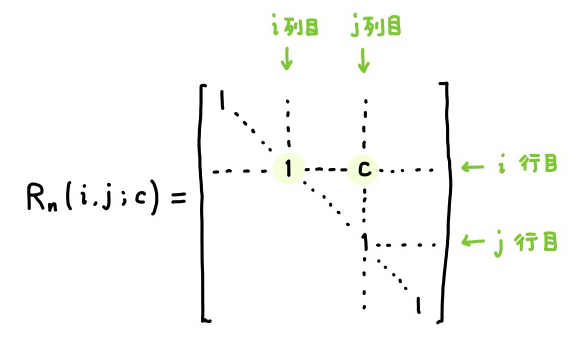
行列 \(A\) の「\(i\) 行目に \(j\) 行目の \(c\) 倍を加える」基本変形では、次の基本行列 \(R_n(i,j;c)\) を、\(A\) の左からかけます。

行列 \(A\) の「\(i\) 列目に \(j\) 列目の \(c\) 倍を加える」基本変形では、次の基本行列 \(R_n(i,j;c)\) を、\(A\) の左からかけます。