微分係数と導関数

いま、\(y\) が \(x\) の関数 \(f(x)\) で与えられているとします。 \(y=f(x)\) のグラフは次のようであるとします。

ここで、この \(y\) がどのように変化しているか考えましょう。

全体的にはギュ～～ン、と右肩上がりになっているのは明らかですが、もう少しきめ細かく、どの時点でどのくらいの増加量があるか、ということを調べてみましょう。

ある \(x = x_0\) を基点として、\(x\) が \(\Delta x\) だけ変化したとします。

\(\Delta\) (デルタ) という記号はしばしば「ちょっと増えた分量」を表します。「Δ (デルタ) とは？」をみてください。

\(x\) が \(x_0\) から\(x_0 + \Delta x\) に変わると、それに伴って \(y\) も \(f(x_0)\) から \(f(x_0 + \Delta x)\) に変わります。つまり、 \(y\) の増加分 \(\Delta y\) は \(\Delta y = f(x_0 + \Delta x) - f(x_0)\) と書けます。

グラフに書くと次のようになります。

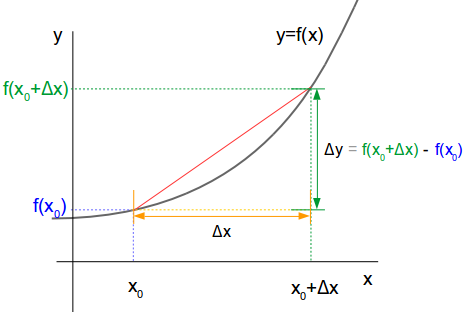
よって \(x = x_0\) から \(x = x_0 + \Delta x\) までの \(y\) の平均変化率は、次のように書けます。

\[ \begin{aligned} \text{y \small{の平均変化率}} &= \frac{y \text{\small{ の増加分}}}{x \text{\small{ の増加分}}}\\ &= \frac{\Delta y}{\Delta x}\\ &= \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} \end{aligned} \]

これは上図の赤い直線の傾きに等しくなります。

さて、\(x = x_0\) から \(x = x_0 + \Delta x\) までの \(y\) の平均変化率としては、これでいいのですが、 \(x = x_0\) のときの変化率はいくらか？というのは、どのようにすればわかるでしょうか。

車で移動しているときの速度に例えてみましょう。\(y\) を進んだ道のり、\(x\) をかかった時間とします。 1 時間で 10 km 移動したとしたら、その 1 時間の平均速度は 10km/h といえます。

しかし、実際の車で考えれば 1 時間、ずっと同じスピードで走るわけではないですよね。移動途中には信号待ちしている時間もあるでしょうし、コンビニやガソリンスタンドで停車したかもしれません。車の速度は途中 50km/h で走っている時もあるでしょうし、5 km/h でノロノロ走っているときもあるでしょう。

平均速度の "10km/h" という値だけでは、その車の速度が分かったことにはなりません。ある瞬間の速度計を見ないとその車の速度はわかりません。

\(y\) の平均変化率を考えるのではなく、ある \(x = x_0\) での \(y\) の変化率を調べるということは、その瞬間の速度計をみることに相当します。

\(x = x_0\) のときの変化率を求めるには、\(\Delta x\) をどんどん小さく、限りなく \(0\) に近付ければよいのです。これには、上の式で \(\Delta x \to 0\) とします。

\[ \begin{aligned} \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} &= \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} \end{aligned} \]

この値のことを、\(f(x)\) の \(x = x_0\) における微分係数といい、次のように書きます。

\[ \begin{aligned} f'(x_0) &= \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} \end{aligned} \]

\(\Delta x\) の代わりに、\(h\) と書けば次のように書けます。

\[ \begin{aligned} f'(x_0) &= \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \end{aligned} \]

あるいは増分で表さずに、\(x = x_0\)、\( w = x_0 + \Delta x\) とおけば、次のようにも書けます。

\[ \begin{aligned} f'(x_0) &= \lim_{w \to x} \frac{f(w) - f(x_0)}{ w - x_0} \end{aligned} \]

どれも意味は同じです。

グラフで考えると、\(x = x_0\) での接線の傾きと微分係数は等しくなります。

上の例で \(f(x) = x^2\) としたときの、\(x = x_0\) における微分係数を求めよ。

定義の式にあてはめて計算します。

\[ \begin{aligned} f'(x_0) &= \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}\\ &= \lim_{\Delta x \to 0} \frac{(x_0 + \Delta x)^2 - x_0^2}{\Delta x}\\ &= \lim_{\Delta x \to 0} \frac{x_0^2 + 2 x_0 \Delta x + (\Delta x)^2 - x_0^2}{\Delta x}\\ &= \lim_{\Delta x \to 0} \frac{2 x_0 \Delta x + (\Delta x)^2}{\Delta x}\\ &= \lim_{\Delta x \to 0} ( 2 x_0 + \Delta x )\\ &= 2 x_0 \end{aligned} \]

導関数とは

上の微分係数の式では、ある \(x = x_0\) という点を考えましたが、任意の \(x\) と考えれば、\(x_0\) を \(x\) を書き換えて次の式を得ます。

\[ \begin{aligned} f'(x) &= \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} \end{aligned} \]

これは \(f(x)\) の導関数といいます。導関数に特定の \(x\) の値を代入すれば、微分係数が得られることになります。

「関数 \(f(x)\) の導関数を求める」ことを単に「\(f(x)\) を微分する」といいます。関数 \(f(x)\) を変数 \(x\) で微分することは、次のようにも書きます。

\[ \frac{d}{dx} f(x) \]

また上記の場合 \(y=f(x)\) なので、単に

\[ \frac{dy}{dx} \]

とも書きます。

微分の書き方はその他にも何種類かあります。考え方は一緒です。

さらに、「関数 \(f(x)\) を \(x\) で微分して \(x = x_0\) を代入して \(x = x_0\) での微分係数を求める」という一連の流れは、次のように縦棒を使って書くこともあります。

\[ \frac{d}{dx} f(x) \Big\vert_{x = x_0} \]

この書き方は、日本の高校のテキストにはあまり出てこないようですが、アメリカの高校のテキストなどでは普通に出てきます。