f の勾配が等位面に垂直であるのはなぜか
\(f(x,y,z)\) のスカラー場で、\(\nabla f\) は等位面に垂直になります。 これがなぜそうわかるのか、説明します。
等位面については「等位面とは?」をみてください。
\(f(x,y,z) = c \) (\(c\) は定数) という等位面を考えます。
この等位面上の任意の曲線を \(t\) をパラメータとして、次のように書きます。
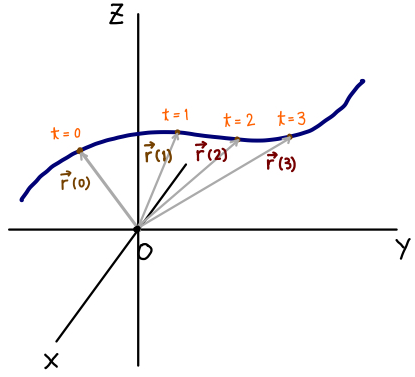
少し言い方を変えれば「等位面上の任意の曲線上の任意の点の位置ベクトルを \(\overrightarrow{r}\) と書く」ということになります。 ベクトル解析で「曲線の式」と言ったら、この式を思い浮かべるといいです。一本の空間曲線を描いて、\(t\) の値が変わると、その曲線上の他の点に移動するイメージです。
さて、\(f(x,y,z) = c \) を \(t\) で微分すると、次のようになります。
\[ \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt} + \frac{\partial f}{\partial z}\frac{dz}{dt} = 0 \]
ここで、これを2つのベクトルの内積とみなして書き換えると、次のようにかけます。
\[ \Big\langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\Big\rangle \cdot \Big\langle \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \Big\rangle = 0 \]
ベクトルの内積はベクトルの成分毎に掛け算して、足し合わせるのでしたね。
ここで、
\[ \Big\langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\Big\rangle \]
というのは、そもそも
\[ \frac{\partial f}{\partial x} \overrightarrow{i} + \frac{\partial f}{\partial y} \overrightarrow{j} + \frac{\partial f}{\partial z} \overrightarrow{k} \]
の成分表示のことですから、
\[ \Big\langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\Big\rangle = \nabla f \]
です。
これは定義そのものです。「ベクトルの勾配」
また、上で定義した \(\overrightarrow{r}(t)\) を \(t\) で微分すると、
\[ \begin{aligned} \frac{\overrightarrow{r}(t)}{dt} &= \frac{x(t)}{dt} \overrightarrow{i} + \frac{y(t)}{dt} \overrightarrow{j} + \frac{z(t)}{dt} \overrightarrow{k}\\ &= \Big\langle \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \Big\rangle \end{aligned} \]
です。
\(\overrightarrow{r}(t) = x(t) \overrightarrow{i} + y(t) \overrightarrow{j} + z(t) \overrightarrow{k}\) を \(t\) で微分するには、 成分ごとに微分して、 \(\overrightarrow{r}'(t) = x'(t) \overrightarrow{i} + y'(t) \overrightarrow{j} + z'(t) \overrightarrow{k}\) です。
つまり、
\[ \Big\langle \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\Big\rangle \cdot \Big\langle \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \Big\rangle = 0 \]
というのは、次の式のことです。
\[ \nabla f \cdot \frac{d\overrightarrow{r}}{dt} = 0 \]
ここで、\(\displaystyle\frac{d\overrightarrow{r}}{dt}\) は等位面上の任意の曲線の接線ベクトルです。
「空間曲線の単位接線ベクトル」も参考にしてください。
曲線の接線ベクトルと勾配 \(\nabla f\) の内積が \(0\) ということは、これらが垂直であるということです。
すなわち、\(\nabla f\) は等位面上の任意の曲線に垂直なので、\(\nabla f\) は等位面に垂直であることがわかります。