面積分

スカラーの面積分

閉曲線で囲まれた滑らかな曲面 \(S\) で、連続なスカラー関数 \(f\) が定義されているとします。このとき \(S\) を \(n\) 個の微小部分に分割し、\(i\) 番目の区画の面積を \(\Delta S_i\)、その中の任意の点を \(P_i\) としたときに、次の和の極限を曲面 \(S\) 上の \(f\) の面積分 (surface integral) といいます。

面積分

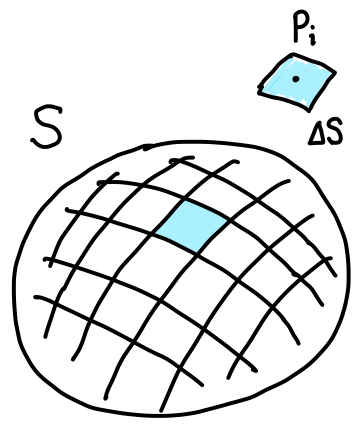
曲面 \(S\) 上の \(f\) の面積分

\[ \lim_{n \to \infty} \sum^n_{i=1} f(P_i) \Delta S = \int_S f dS \]

\(f = 1\) のとき、面積分の値は \(S\) の面積になります。

ベクトルの面積分

\(\overrightarrow{F}\) のベクトル場の中で上記の曲面 \(S\) が定義されているとします。

この時、\(S\) の微小部分における \(\overrightarrow{F}\) の法線方向成分 \(F_n\) は、単位法線ベクトルを \(\overrightarrow{n}\) として、\(F_n = \overrightarrow{F} \cdot \overrightarrow{n}\) と書けます。

面積分

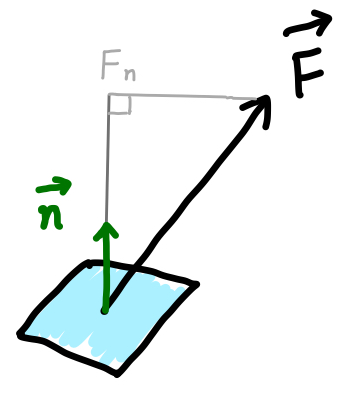
つまり、\(\overrightarrow{F} \cdot \overrightarrow{n}\) というのは「ベクトル \(\overrightarrow{F}\) の \(S\) の法線方向成分を取り出す」という操作です。ですから、スカラー関数 \(F_n(x,y,z) = \overrightarrow{F} \cdot \overrightarrow{n}\) としたら「\(F_n\) は \(S\) での \(\overrightarrow{F}\) の法線成分量の分布を表すスカラー関数」になります。

上で見た面積分の式を \(F_n\) で書き換えると、

\[ \begin{aligned} \lim_{n \to \infty} \sum^n_{i=1} F_n(P_i) \Delta S &= \int_S F_n dS\\ &= \int_S \overrightarrow{F} \cdot \overrightarrow{n} dS \end{aligned} \]

こうして計算した量を、ベクトル関数 \(\overrightarrow{F}\) の面積分といいます。

ベクトル関数を面積分するというのは、ベクトルそのものを何か足し合わせていくような操作をするわけではなくて、法線成分を取り出して作るスカラー量の面積分 (足し算) をする、ということなのです。

なお、\(\overrightarrow{n} dS\) を法線方向向きの大きさ \(dS\) のベクトルとして、\(d\overrightarrow{S}\) と書いて 面積ベクトル などとも言います。

面積ベクトルを使って書くこともあり、この場合、面積分は次の式になります。

\[ \int_S \overrightarrow{F} \cdot \overrightarrow{n} dS = \int_S \overrightarrow{F} \cdot d\overrightarrow{S} \]