主法線ベクトルと曲率半径

ある曲線とある点での接触平面を考えます。

接触平面上の曲線上に二点 P , Q をとり、それぞれの位置ベクトルを \(\overrightarrow{r}(s)\)、\(\overrightarrow{r}(s+\Delta s)\) とします。 そして P, Q の二点を通る円を考えます。(この円も接触平面上に乗っています)

この円の中心を \(O\)、半径を \(\rho\) として、 \(\angle POQ\) を \(\Delta \theta\) とすると、弧長は \(\Delta s = \rho \Delta \theta \) と書けます。

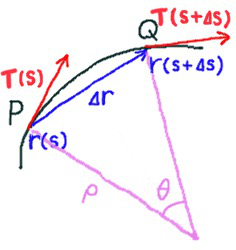
点 P での単位接線ベクトル \(\overrightarrow{t}\) は \(s\) を用いて、\(\overrightarrow{t}(s) = \displaystyle\frac{ d\overrightarrow{r} }{ds} \) と書けます。

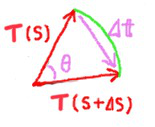
点 Q での単位接線ベクトルは \(\overrightarrow{t}(s + \Delta s)\) で、その差を \(\Delta \overrightarrow{t}\) と書くと

\[ \Delta \overrightarrow{t} = \overrightarrow{t}(s + \Delta s) - \overrightarrow{t}(s) \]

です。一方、緑色で示した弧の長さは \(| \overrightarrow{t} | \Delta \theta \) ですが \(| \overrightarrow{t} | = 1\) なので、弧の長さは \(\Delta \theta\) です。 「空間曲線の単位接線ベクトル」 でみたように \(\Delta \theta \to 0\) のとき、弧と弦の長さは等しくなるので結局、次がわかります。

\[ | \Delta \overrightarrow{t} | = | \overrightarrow{t}(s + \Delta s) - \overrightarrow{t}(s) | = \Delta \theta \]

以上から次の関係がわかります。

ここで微小変化 \(\Delta s\) を限りなく小さくすれば

\[ \lim_{\Delta s \to 0} \frac{\Delta \overrightarrow{t}}{\Delta s} = \frac{d \overrightarrow{t}}{ds} \]

ですから、上の式は次のように書直せます。

また \(\overrightarrow{t}(s)\) は単位長の接線ベクトルなので、\(\overrightarrow{t} \cdot \overrightarrow{t} = 1\) を \(s\) で微分することで、次の関係がわかります。

従って、\(\overrightarrow{t}\) と \(\displaystyle\frac{d\overrightarrow{t}}{ds}\) は直交することがわかります。

以上から \(\displaystyle\frac{d\overrightarrow{t}}{ds}\) は向きが接線ベクトル \(\overrightarrow{t}\) と垂直方向であり、大きさが \(\displaystyle\frac{1}{\rho}\) のベクトルであることがわかりました。 従って、 \(\overrightarrow{n}\) を単位法線ベクトルとすると次の関係としてかけます。

特にこの接触平面内の法線ベクトルを主法線ベクトルといいます。

また、この \(\rho\) は曲率半径というのですが、これについてはさらに「曲率と曲率半径」をみてください。