捩率と従法線ベクトル

「法線ベクトルと曲率半径」では、主法線ベクトル \(\overrightarrow{n}\) について説明しました。これは単位接線ベクトルを \(s\) で微分して、曲率半径をかけたものに等しいです。

\[ \overrightarrow{n} = \rho \frac{d \overrightarrow{t}}{ds} \]

接線ベクトルと主法線ベクトルは接触平面内にあります。

ここで、接触平面に垂直となるベクトルを次のように定義します。

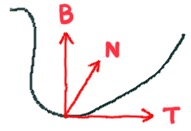
\[ \overrightarrow{b} = \overrightarrow{t} \times \overrightarrow{n} \]

これで定義される \(\overrightarrow{b}\) を従法線ベクトルといいます。 \(\overrightarrow{t}\) も \(\overrightarrow{n}\) も単位ベクトルなので、\(\overrightarrow{b}\) の大きさも単位長になります。

ベクトル積の大きさについては「ベクトル積の大きさは平行四辺形の面積」をみてください。

さて、接触平面というのは、局所的にその曲線が乗っている平面のことでした。ここで定義した従法線ベクトルは、接触平面に垂直なベクトルです。

もし、曲線全体がある平面に乗っていたら、従法線ベクトルは変わりません。いつでも長さ 1、接触平面に垂直のままです。

ところが、もし曲線が平らな平面に乗らない場合は、従法線ベクトルはグラグラと動くことになります。

従って、\(\overrightarrow{b}\) の変化率 \(\tau\) を次の式で定義します。

\[\Big| \frac{ d\overrightarrow{b} }{ds}\Big| = | \tau | \]

\(\tau\) はどのくらい平らな平面にのらないかという物差しに使えます。 \(\tau\) は捩率 (れいりつ) といいます。捩という時は、ねじる (捩る) と読め、捩率は「捩れ率」ともいいます。

\(\tau\) はギリシャ文字でタウと読みます。

さて、\(\overrightarrow{b} = \overrightarrow{t} \times \overrightarrow{n} \) を \(s\) で微分すると、

\[ \begin{aligned} \frac{d\overrightarrow{b}}{ds} &= \frac{d\overrightarrow{t}}{ds} \times \overrightarrow{n} + \overrightarrow{t} \times \frac{d\overrightarrow{n}}{ds}\\ &= \frac{1}{\rho} ( \overrightarrow{n} \times \overrightarrow{n} ) + \overrightarrow{t} \times \frac{d \overrightarrow{n}}{ds}\\ &= \overrightarrow{t} \times \frac{d\overrightarrow{n}}{ds} \end{aligned} \]

また \(\overrightarrow{b} \cdot \overrightarrow{b} = 1\) を \(s\) で微分すると、\(\displaystyle\frac{d\overrightarrow{b}}{ds} \cdot \overrightarrow{b} = 0\) 。

この結果より、\(\displaystyle\frac{d\overrightarrow{b}}{ds} \) は \(\overrightarrow{t}\) 及び \(\overrightarrow{b}\) の両方に垂直であるから、向きは \(\overrightarrow{n}\) と同一。

大きさは \(| \tau |\) でしたが、符号は次の向きに定義します。

\[ \frac{d\overrightarrow{b}}{ds} = - \tau \overrightarrow{n} \]

これが主法線ベクトルと従法線ベクトルの変化率との関係になります。