二項定理

ここでは二項定理 (binomial theorem) について説明します。

二項定理ではいきなりちょっとヤヤコシそうな式が出てきます。いきなり結論に飛びつくとたいていの人は「ウッ」とひるみます。まずは、ちょっとウッとなってもらいましょう（笑）

\[ \begin{aligned} (a + b)^n &= \sum_{r = 0}^{n} \binom{n}{r} a^{n-r} b^r \end{aligned} \]

というのが二項定理で、二項係数の性質として出てくるのが

\[ \binom{n}{r} = \binom{n-1}{r-1} + \binom{n-1}{r} \]

などです。

こんな式を丸暗記していたら体が持たないので、式の意味を理解して自然と導けるようにする、というのが、このページの狙いです。

それでは順番に説明していきます。

準備：組み合わせ \({}_n C_r\)

前提となる知識はこれだけ。組み合わせの数だけです。\(n\) 個の異なるものから \(r\) 個取り出すときの組み合わせの数 (コンビネーション数) は、次の式で表されます。

\[ {}_{n} C_{r} = \frac{n!}{r! (n-r)!} \]

また、これは次のように縦書きにも書きます。意味は同じです。

\[ {}_{n} C_{r} = \binom{n}{r} \]

この式の導き方については「組み合わせ」をみてください。

以上が前提知識です。さっそく二項定理をみてみましょう。

二項定理

二項定理は \((a+b)^n\) を多項式に展開する方法を示しています。

多項式に展開するということは、例えば \(n=2\) のとき \((a+b)^2 = (a+b)(a+b)\) ですが、2個ある \((a+b)\) から、 \(a\) か \(b\) かいずれかの項を選んで掛け算して、その結果の和をとることになります。

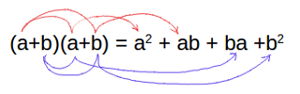
一個目の \((a+b)\) から \(a\) を選び、二個目の \((a+b)\) からも \(a\) を選んで掛け算した結果が \(a^2\) という項です。一個目の \((a+b)\) から \(a\) を選び、二個目の \((a+b)\) からは \(b\) を選んで掛け算した結果は \(ab\)。一個目の \((a+b)\) から \(b\) を選び、二個目の \((a+b)\) からは \(a\) を選んで掛け算した結果は \(ba\) 。一個目の \((a+b)\) から \(b\) を選び、二個目の \((a+b)\) からも \(b\) を選んで掛け算した結果は \(b^2\) ・・・という調子です。

\(ab\) と \(ba\) は等しいのでまとめ上げると、結局、

\[ (a+b)(a+b) = a^2 + ab + ba + b^2 = a^2 + 2ab + b^2\]

となります。

\(n\) 乗の場合も同様に考えます。

\[ \begin{aligned} (a+b)^n &= \underbrace{ (a+b) \cdot (a+b) \cdot \cdots \cdot (a+b) \cdot (a+b) }_{ \small{(a+b)} \text{\footnotesize{が}} \small{n} \text{\footnotesize{個}} } \end{aligned} \]

\(n\) 個の \((a+b)\) から、それぞれ \(a\) または \(b\) を選んで掛け合わせて項を作ります。\(a\)、\(b\) 合わせて \(n\) 回選ぶので、 \(b\) を \(r\) 回選んだら \(a\) は \(n-r\) 回選ぶことになります。

また、\(n\) 個の \((a+b)\) から \(b\) を \(r\) 回選ぶ選び方は、組み合わせの考え方から \(\displaystyle\binom{n}{r}\) 個とわかります。つまり、 \(a^{n-r} b^r\) という項は \(\displaystyle\binom{n}{r}\) 個出現します。

\(r\) は \(0\) から \(n\) までとりうるので、結局、上の式は次のようにかけます。

\[ \begin{aligned} (a+b)^n &= \binom{n}{0} a^n + \binom{n}{1} a^{n-1}b + \binom{n}{2} a^{n-2} b^2 + \cdots \\ &+ \binom{n}{r} a^{n-r}b^r + \cdots + \binom{n}{n-1} ab^{n-1} + \binom{n}{n} b^{n}\\ &= \sum_{r = 0}^{n} \binom{n}{r} a^{n-r} b^r \end{aligned} \]

この式が二項定理になります。

\(\displaystyle\binom{n}{r}\) はコンビネーション \({}_n C_r\) に等しいのですが、二項定理で出てくるときは特に二項係数ともいいます。

二項係数の関係式はパスカルの三角形で考える

パスカルの三角形というのは次のような数値の並びをいいます。

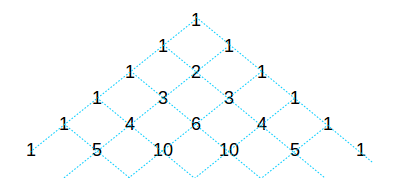
同じ段の左右を足し合わせることで、下の段の数字が決まります。

さて、これが二項定理となんの関係があるのでしょうか。

上の説明では二項係数 \(\displaystyle\binom{n}{r}\) は \(n\) 個の\((a+b)\) の掛け合わせで、 \(b\) を \(r\) 個選ぶ回数であると説明しました。

三角形の段を降りるときに、\(a\) を選ぶなら左、\(b\) を選ぶなら右に進む、と取り決めます。

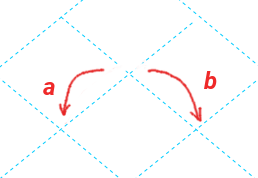
すると以下の関係になるのです。

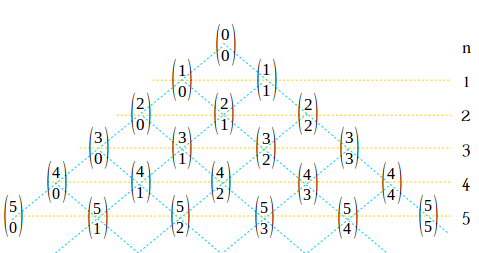
これがなぜか、 \(\displaystyle\binom{4}{2}\) に着目して具体的に考えてみましょう。

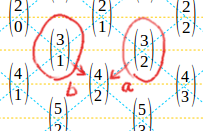
\(\displaystyle\binom{4}{2}\) は \(4\) 個から \(2\) 個 \(b\) を選ぶときの、組み合わせの数を表しています。これは『 \(3\) 個から、まだ \(1\) 個しか \(b\) を選んでおらず、\(4\) 個目で \(b\) を選んで \(\displaystyle\binom{4}{2}\) に到達する場合の「組み合わせの数」 \(\displaystyle\binom{3}{1}\) 』と『\(3\) 個から既に \(2\) 個 \(b\) を選んでおり、\(4\) 個目に \(a\) を選んで \(\displaystyle\binom{4}{2}\) に到達する場合の組み合わせの数 \(\displaystyle\binom{3}{2}\) 』との足し合わせになります。

\[ \binom{4}{2} = \binom{3}{1} + \binom{3}{2} \]

これを一般化して考え、\(\displaystyle\binom{n}{r}\) に至る経路に着目して図にすると次の通りです。

この関係から、次の式が導かれます。

\[ \binom{n}{r} = \binom{n-1}{r-1} + \binom{n-1}{r} \]

以上、二項定理と係数の意味について説明しました。

冒頭にあげた式の意味が、クリアになったでしょうか。