ガウスの発散定理

\(\overrightarrow{F}\) のベクトル場で、閉曲面 \(S\) と、\(S\) で囲まれた領域 \(V\) を考えます。 このとき、\(\overrightarrow{n}\) を \(S\) の単位法線ベクトルとします。

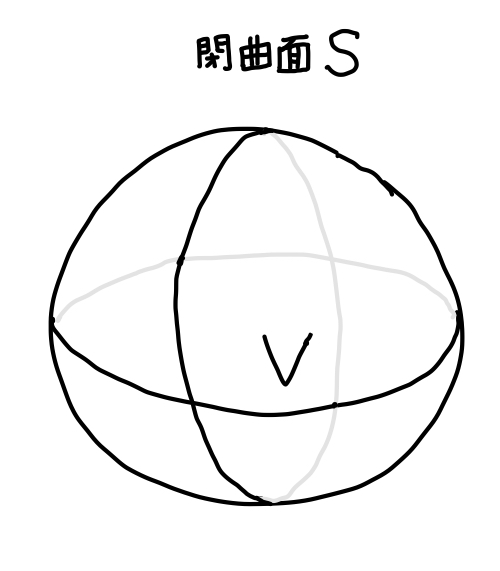
このとき体積分と面積分の関係を表す次の関係を、ガウスの発散定理 (Gauss's divergence theorem) といいます。

発散定理の意味は？

さて、この意味はどういうことでしょうか？

\(\nabla \cdot \overrightarrow{F} = \text{div}\overrightarrow{F}\) ですから、この左辺は「発散の体積分」です。 発散は「ベクトルの発散」でみたように「単位時間、単位体積からの流出量」です。

\[ \begin{aligned} \text{\small{左辺}} &= \int_V \text{div} \overrightarrow{F} dV\\ &= \int_V (\text{\footnotesize{単位時間、単位体積からの流出量}}) dV\\ &= \text{\small{V からの単位時間の流出量}} \end{aligned} \]

一方、右辺をみると、こちらは体積分ではなく、面積分です。

ベクトルの面積分はベクトル場 (水流などの速度のベクトル場をイメージしてください) の \(S\) 上のベクトルの法線成分を積分、つまり足し合わせます。

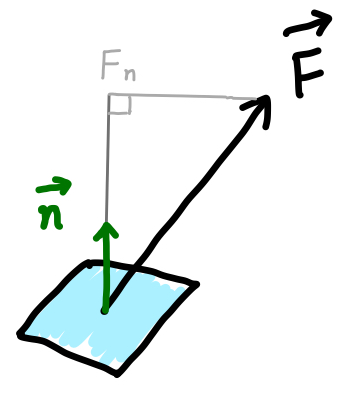
つまり、

ということになります。

つまり、発散定理は \(V\) からの流出量は、その表面である \(S\) を通って出てくる量に等しい、ということを述べているのです。

発散定理の形式的な覚え方は？

発散定理の意味自体は上で説明した通りで、直感的にもわかりやすい状況を述べています。

ただ、この意味だけ覚えていても、数学としてあまり役に立ちませんよね。しっかり式自体も覚え、体積分を面積分に、あるいは、その逆に面積分を体積分に書き換えたりすることで、 計算を簡単に済ませることができるようになりましょう。

さて、もう一度、発散定理の式をみてみましょう。

\[ \int_V \nabla \cdot \overrightarrow{F} dV = \int_S \overrightarrow{F} \cdot \overrightarrow{n} dS \]

内積は一般に \(\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{b} \cdot \overrightarrow{a}\) ですから、\(\overrightarrow{F}\) と \(\overrightarrow{n}\) の順番を変えることができます。

\[ \int_V \nabla \cdot \overrightarrow{F} dV = \int_S \overrightarrow{n} \cdot \overrightarrow{F} dS \]

すると互いに、「\(S\) と \(V\)」 並びに 「\(\nabla\) と \(\overrightarrow{n}\) 」を書き換えた式になっていることがわかります。

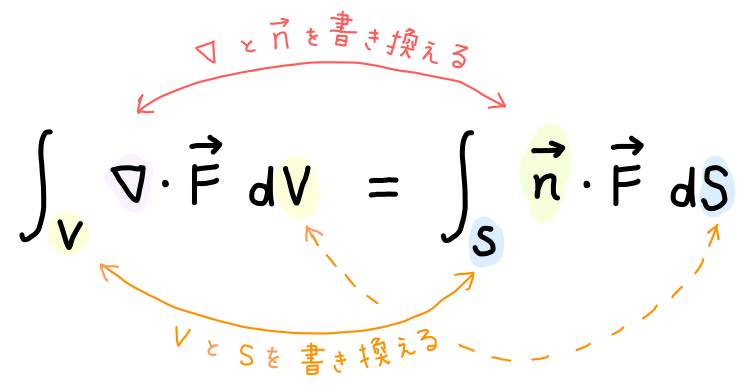
このように、形式的にも式変換をできるようにしておくと、問題を解くときなどに便利です。