逆関数の微分公式 問題(1)
\(f(x)=5x^3+x+2\) のとき \((f^{-1})'(2)\) を求めよ。
この問題を解くには次の公式が役に立ちます。
\[
(f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}
\]
この公式の意味については「逆関数の微分公式」を参考にしてください。
この公式を知っているものとして、上の問題を解いてみましょう。
上の公式から \(x=2\) のとき、次が関係が成り立ちます。
\[ \tag{A} (f^{-1})'(2) = \frac{1}{f'(f^{-1}(2))} \]
ここで右辺の分母に現れる、\(f^{-1}(2)\) というのは、「関数 \(f(x)\) の値を \(2\) とする \(x\)」のことです。
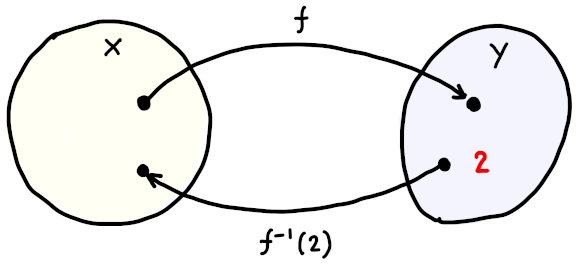
従って \(f(x) = 2\) を満たす \(x\) を求めます。
\[
\begin{aligned}
f(x) = 5x^3+x+2 &= 2\\
5x^3+x &= 0\\
x (5x^2+1) &= 0\\
\therefore \ x = 0
\end{aligned}
\]
(注: \(5x^2+1\) は実数の範囲で \(0\) にならないので \(x=0\) です。)
よって、\(f^{-1}(2) = 0\) ですから、上の (A) 式は次になります。
\[ \tag{B} (f^{-1})'(2) = \frac{1}{f'(0)} \]
ここで \(f'(x) = 15x^2 + 1\) ですから、\(f'(0) = 1\) です。これを (B)式に代入すると次が得られます。
\[ (f^{-1})'(2) = \frac{1}{1} = 1 \]
これで上の問題の答えは得られました。