数列の和問題 (1)

次の和を求めよ。

\[ 0 + 3 + 8 + 15 + 24 \]

ただの足し算の問題と考えれば、電卓を使って足し算すれば終了です。

でもそれは、今回はたまたま 5 項しかないから電卓を使って計算すると速いだけです。もしこれが 100 項もあったら、電卓を使って単純な足し算をしていくより、規則を持った数列の和として考えて計算した方が素早く、正確に計算することができるでしょう。

ここでも、数列の和の問題として考えます。

下記の式変形で使うので、数列の和の公式を先に書いておきます。

\[ \begin{aligned} \sum_{k=1}^{n} k &= \frac{n(n+1)}{2}\\ \sum_{k=1}^{n} k^2 &= \frac{n(n+1)(2n+1)}{6} \end{aligned} \]

公式については「数列の和の公式」をみてください。

数列 \(\{a_n\} = 0, 3, 8, 15, 24, \cdots\) を考えます。これは

\[ 1^2-1, 2^2-1, 3^2-1, 4^2-1, 5^2-1, \cdots \]

と等しいので、 \(n = 1, 2, 3, \cdots \) としたとき \(n\) 項目は \(a_n = n^2 - 1\) となる。

従って、数列 \(\{a_n\}\) の第 \(1\) 項から \(n\) 項までの和 \(S_n\) は次のように書けます。

\[ \begin{aligned} S_n &= \sum_{k = 1}^n a_k \\ &= \sum_{k = 1}^n (k^2 - 1)\\ &= \sum_{k = 1}^n k^2 - \sum_{k = 1}^n \cdot 1\\ &= \frac{n(n+1)(2n+1)}{6} - n\\ &= \frac{n(n-1)(2n+5)}{6} \end{aligned} \]

よって、\(a_5\) までの和 \(S_5\) は上式で \(n = 5\) として、

\[ \begin{aligned} S_5 &= \frac{ 5 \times ( 5 - 1 ) \times ( 2 \times 5 + 5 ) }{6} \\ &= \frac{ 5 \times 4 \times 15 }{6} \\ &= 50 \end{aligned} \]

以上で終了ですが、もうひとつ解答を書いておきます。

上で数列 \(\{a_n\}\) の一般項は \(a_n = n^2 - 1\) ですが、不運にも次のような数列として考えてしまった時の計算です。

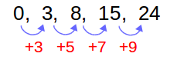
この場合は、計算がちょっとだけ面倒なことになります。

数列 \(\{a_n\} = 0, 3, 8, 15, 24, \cdots\) を考えます。 \(a_{n+1} - a_{n}\) の数列、すなわち \(\{a_n\}\) の階差数列は \(\{b_n\} = 3, 5, 7, 9, \cdots \) です。

\(\{b_n\}\) の一般項は初項 \(3\) 公差 \(2\) の等差数列なので、\(b_n = 3 + 2(n-1) = 2n + 1\) と書ける。

さて \(n \ge 2\) のとき

\[ \begin{aligned} a_2 &= a_1 + b_1\\ a_3 &= a_2 + b_2 = a_1 + b_1 + b_2 \\ a_4 &= a_3 + b_3 = a_1 + b_1 + b_2 + b_3\\ \cdots \\ a_n &= a_1 + \sum_{k=1}^{n-1} b_k\\ &= a_1 + \sum_{k=1}^{n-1} (2k+1)\\ &= a_1 + 2 \sum_{k=1}^{n-1} k + \sum_{k=1}^{n-1} \cdot 1\\ &= 0 + 2 \cdot \frac{(n-1) n}{2} + n-1\\ &= n^2 - n + n -1 \\ &= n^2 - 1 \end{aligned} \]

\(n=1\) のとき \(a_1 = 0\) であるから、上で求めた一般項 \(a_n = n^2 - 1\) は \( n \ge 1\) で成り立つ。

この後は最初の解答と同様。

\(a_n = n^2 - 1\) ということに、うまくすぐに気付けばそれをスタート地点にできますが、不運にも階差数列を使う方向に考えてしまうと、ちょっと面倒なことになってしまいますね。

数列の和 問題 (1)

数列の和問題 (1)