三角関数に慣れる (1)
ここでは直角三角形の斜辺とその他 1 辺とがなす角を \(\theta\) としたときに、 斜辺の長さでその他 2 辺を表す方法について説明します。
一度わかってしまえばとても簡単で、応用が効くので、まだ慣れていない人はぜひ慣れてください。
次のような直角三角形を考えます。斜辺の長さを \(A\)、斜辺ともう 1 辺となす角を \(\theta\) としています。
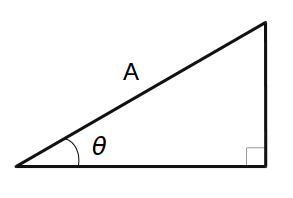
このとき、他の 2 辺の長さはそれぞれ \(A \cos \theta\)、\(A \sin \theta\) と書けます。
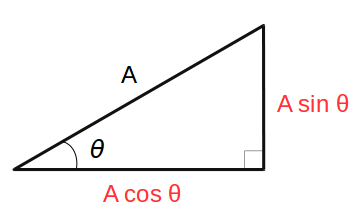
これだけのことです。
「三角関数」では次の図を使って、\(\sin \theta\) と \(\cos \theta\) の説明をしました。
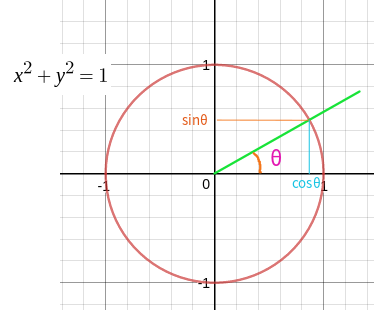
この場合は斜辺の長さ \(A\) が \(1\) のときに相当します。相似三角形で斜辺の長さが \(A\) 倍になれば、他の 2 辺の長さも \(A\) 倍になるので、 それぞれ \(A \cos \theta\)、\(A \sin \theta\) となる、というわけです。
このことを、三角形が逆さまになっても、斜めになってもパッとわかるようにしておきましょう。
少し練習問題です。
下図で \(a\) と \(b\) の長さを求めよ
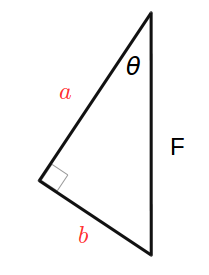
上を理解していれば即答です。
\[a = F \cos \theta \]
\[ b = F \sin \theta \]
下図で \(a\) と \(b\) の長さを求めよ
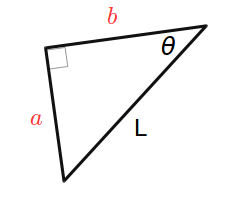
逆さまですがこちらも次のようになります。
\[ a = L \sin \theta \]
\[ b = L \cos \theta \]