フーリエ余弦積分
「フーリエ積分」でみたように、 フーリエ積分は次の式で求められます。
\[ \begin{aligned} f(x) &= \int_0^{\infty} [A(s) \cos sx + B(s) \sin sx] ds\\ A(s) &= \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \cos st dt\\ B(s) &= \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \sin st dt \end{aligned} \]
積分が存在する条件と存在した場合の値については「フーリエ積分の成り立つ条件と値」をみてください。
ここで、\(f(x)\) が偶関数 (even function) である場合を考えましょう。
偶関数というのは、任意の \(x\) で \(f(x) = f(-x)\) が成り立つ関数です。例えば、\(f(x) = x^2\) は偶関数ですが、 絶対値の同じ \(x = \pm a\) では \(f(a) = f(-a)\) です。
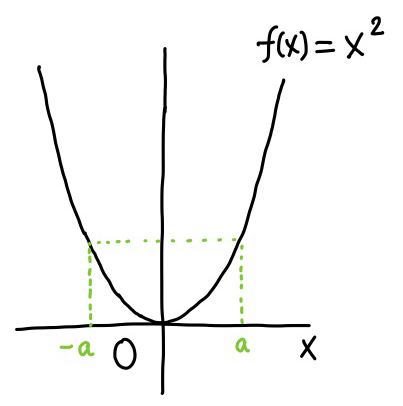
偶関数 \(f(x) = x^2\) や \(f(x) =x^4\) の指数が偶数であることから、偶関数という名前になっているのでしたね。 「偶関数と奇関数の積分」も参考にしてください。
さて、上の \(A(s)\) をみると、被積分関数の \(f(t) \cos st\) は、 \(f(t)\) が偶関数であり、\(\cos st\) も偶関数なので、それらの積である \(f(t) \cos st\) も偶関数です。
よって、
\[ \begin{aligned} A(s) &= \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \cos st dt\\[1.4em] &= \frac{2}{\pi} \int_{0}^{\infty} f(t) \cos st dt \end{aligned} \]
となります。積分区間が半分になって、全体が \(2\) 倍してあります。
一方、\(B(s)\) をみると、被積分関数の \(f(t) \sin st\) は、 \(f(t)\) が偶関数であり、\(\sin st\) が奇関数なので、それらの積である \(f(t) \sin st\) は奇関数です。よって、直ちに
\[ \begin{aligned} B(s) &= \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \sin st dt\\ &= 0 \end{aligned} \]
であることがわかります。
以上をまとめると、次のように書けます。
\(f(x)\) が偶関数である時、フーリエ積分は
\[ \begin{aligned} f(x) &= \int_0^{\infty} A(s) \cos sx ds\\ A(s) &= \frac{2}{\pi} \int_{0}^{\infty} f(t) \cos st dt\\ \end{aligned} \]
とかけます。これをフーリエ余弦積分 (Fourier Cosine Integral) といいます。
ここではフーリエ「余弦」(コサイン) 積分の説明をしました。フーリエ正弦積分 も同様の考え方で理解できます。