フーリエ正弦級数 例題(2)

正弦級数に展開するために \(f(x)\) が、奇関数となるように \(f(x)\) を拡張して考えます。

問題では \(0 \lt x \lt L\) の範囲でしか定義されていませんが、\(f(x)\) が奇関数となるように、下図のように \(-L \lt x \lt 0\) があるものとして考えます。

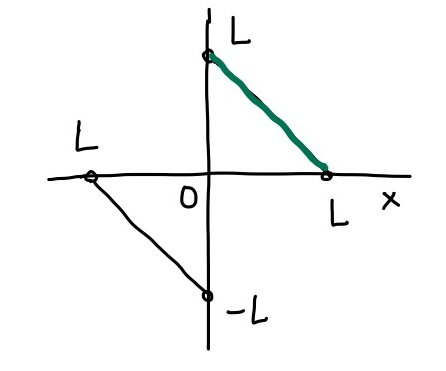
\(f(x)\) が奇関数となれば、フーリエ係数 \(a_n = 0\) \((n=0, 1, \cdots)\) ですから、 \(b_n\) だけ計算すれば良いことになります。

\[ \begin{aligned} b_n &= \frac{2}{L} \int_0^{L} (L - x) \sin \frac{n\pi x}{L} dx\\ &= \frac{2}{L}\Big\{\Big[-\frac{L}{n\pi}(L-x)\cos\frac{n\pi x}{L}\Big]_0^{L} - \int_0^{L}(-1)\Big(-\frac{L}{n\pi}\cos\frac{n\pi x}{L}\Big)dx\Big\}\\ &= \frac{2}{L}\Big\{ -\frac{L}{n\pi}(0 - L) - \frac{L}{n\pi} \int_0^{L} \cos\frac{n\pi x}{L} dx \Big\}\\ &= \frac{2}{L}\Big\{ \frac{L^2}{n\pi} - \frac{L}{n\pi}\Big[ \frac{L}{n\pi}\sin\frac{n\pi x}{L} \Big]_0^{L} \Big\}\\ &= \frac{2}{L}\Big\{ \frac{L^2}{n\pi} - \frac{L^2}{n^2\pi^2} (\sin n\pi - \sin 0) \Big\}\\ &= \frac{2L}{n\pi} \end{aligned} \]

以上から、\(f(x)\) の正弦級数は次のようになります。

\[ \begin{aligned} f(x) &= \sum_{n=1}^{\infty} b_n \sin\frac{n\pi x}{L}\\ &= \sum_{n=1}^{\infty} \frac{2L}{n\pi}\sin\frac{n\pi x}{L}\\ &= \frac{2L}{\pi}\Big( \sin\frac{\pi x}{L} + \frac{1}{2}\sin\frac{2\pi x}{L} + \frac{1}{3}\sin\frac{3\pi x}{L} + \cdots \Big) \end{aligned} \]

試しに MATLAB を使って、 \(L=\pi\) として \(n=10\) までのグラフを描くと、次のようになりました。

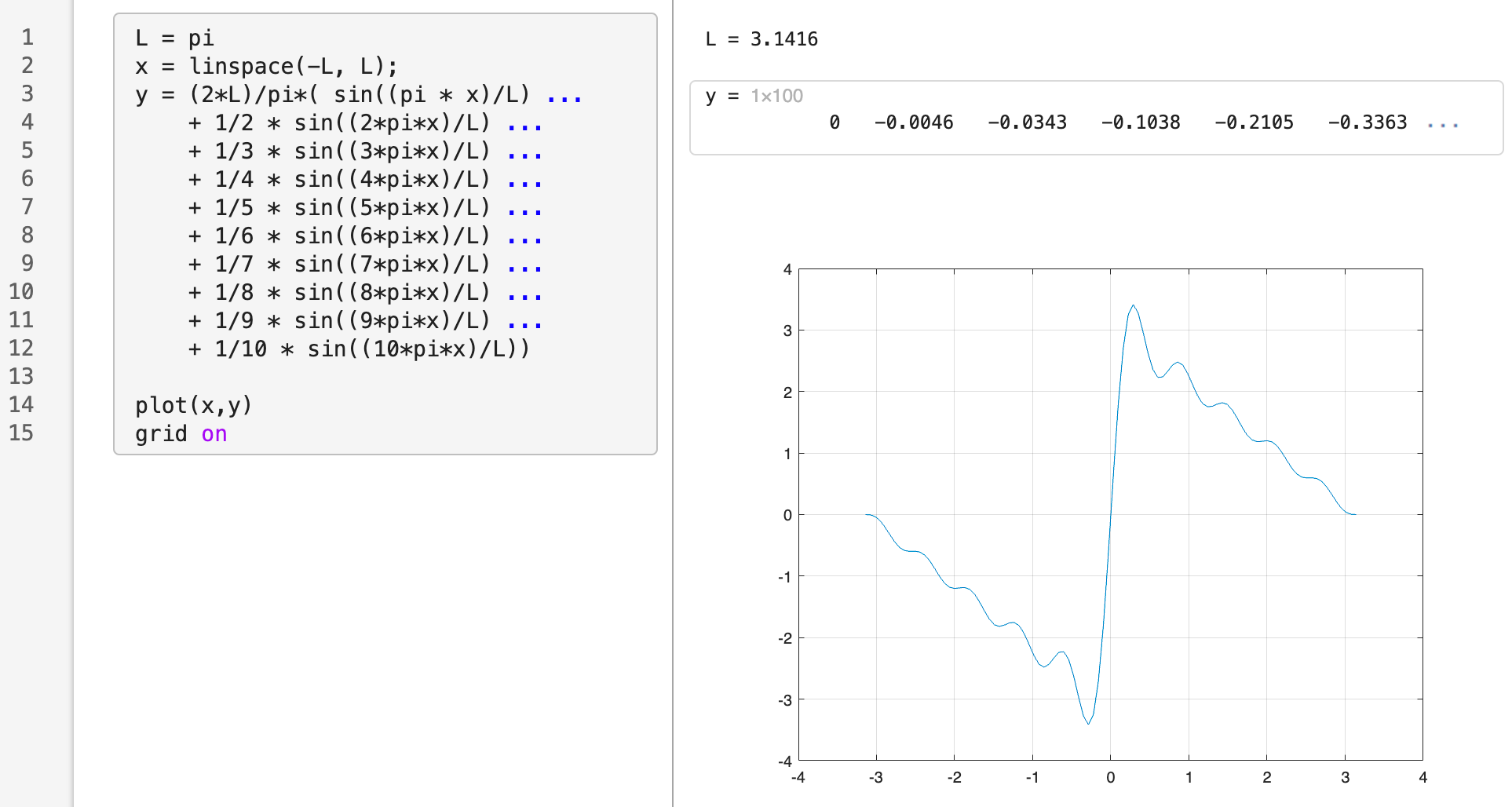
確かに、上で想定したグラフに近い形になっていることが確認できました。

• フーリエ正弦級数 例題(1)
• フーリエ正弦級数 例題(2)