方向余弦 問題 (1)

「方向余弦」でみたように、「\(\overrightarrow{v}\) の方向余弦」というのは 「\(\overrightarrow{v}\) と同じ向きの単位ベクトルの成分」のことです。

問題の \(\overrightarrow{v}\) は \(z\) 成分が \(0\) ですから、\(xy\) 平面に乗っています。

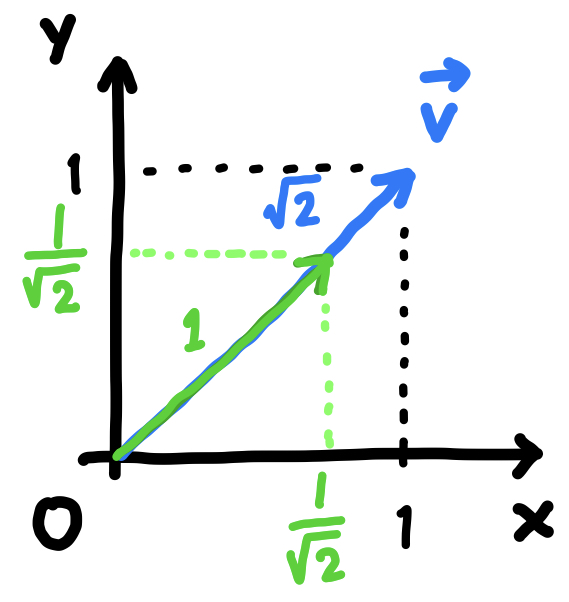
\(\|\overrightarrow{v} \| = \sqrt{1^2+1^2} = \sqrt{2}\) です。

よって、\(\overrightarrow{v}\) と同じ向きの単位ベクトルは次の通りです。

\[ \frac{\overrightarrow{v}}{\|\overrightarrow{v}\|} = \Big\langle \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0 \Big\rangle \]

従って方向余弦は \(\cos \alpha = \cfrac{1}{\sqrt{2}}\)、\(\cos \beta = \cfrac{1}{\sqrt{2}}\)、\(\cos \gamma = 0\) です。

また、このことから方向角 (direction angles) は \(\alpha = 45\degree\)、\(\beta = 45\degree\)、\(\gamma = 90\degree\) であることがわかります。

この例では \(\overrightarrow{v}\) が \(xy\) 平面上にあるので、角度は直感的にも明らかにわかります。

しかし、三次元のベクトルでは簡単な図形でも方向角はキリのいい簡単な数字にはなりません。 次の問題で確かめてみましょう。