方向余弦 問題 (2)

「方向余弦」でみたように、「\(\overrightarrow{v}\) の方向余弦」というのは

「\(\overrightarrow{v}\) と同じ向きの単位ベクトルの成分」

のことです。

問題の \(\overrightarrow{v}\) は長さ \(1\) の立方体の対角線に沿っています。

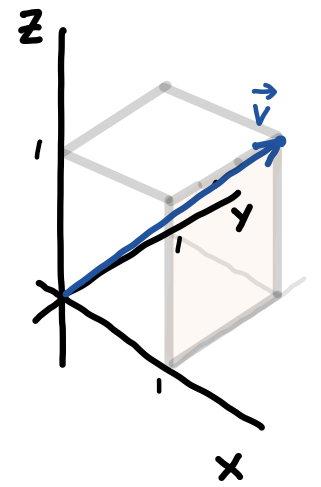
同じ向きの単位ベクトル (長さ \(1\) のベクトル) を求めるには、それ自身の長さで割れば良いです。 \(\overrightarrow{v}\) の長さは、 \(\|\overrightarrow{v} \| = \sqrt{1^2+1^2+1^2} = \sqrt{3}\) です。

よって、\(\overrightarrow{v}\) と同じ向きの単位ベクトルは次の通りです。

\[ \frac{\overrightarrow{v}}{\|\overrightarrow{v}\|} = \Big\langle \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}} \Big\rangle \]

従って方向余弦は \(\cos \alpha = \cfrac{1}{\sqrt{3}}\)、\(\cos \beta = \cfrac{1}{\sqrt{3}}\)、\(\cos \gamma = \cfrac{1}{\sqrt{3}}\) です。

このことから方向角 (direction angles) は \(\alpha \approx 54.74\degree\)、\(\beta \approx 54.74\degree\)、\(\gamma \approx 54.74\degree\) であることがわかります。