空間曲線で扱う主なベクトルと平面

ここで学ぶトピックは空間曲線 (space curves) といいますが、要は普通の３次元空間にある曲線を考えて、それを数式で表していきましょう、ということです。

空間曲線を理解するために、三つのベクトルと三つの面を定義します。

まずは、そのうち一つの平面と三つのベクトルからみていきます。

接触平面と三つのベクトル

下の図では赤い線が三次元空間の曲線を表しています。前提として滑らかな曲線を考えます。

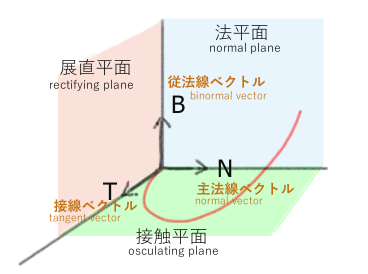
この曲線上のある点に着目します。そして、その曲線上のそばにある他の 2 点を考え、それらが乗っているひとつの平面を考えます。

2 点あれば直線はひとつに決まるように、平面は 3 点あればひとつ決まりますね。

局所的に曲線が乗っている平面を接触平面 といいます。上の図の下の面です。

着目している点における接線は接触平面上にあるので、接線上に単位長さにとった接線ベクトルも接触平面上にあります。接線は英語で Tangent なので、接線ベクトルは \(\bold{T}\) で書きます。小文字で \(\bold{t}\) とする場合もあります。どちらも同じです。

経験的にはアメリカの教科書では大文字を使うことが多く、日本の教科書では小文字を使うことが多いように思います。

また、接触平面上で接線ベクトルに垂直な単位長さのベクトルを 主法線ベクトル といいます。法線は英語で Normal なので、法線ベクトルの記号は \(\bold{N}\) または \(\bold{n}\) です。

さらに、ここで直行している二つのベクトル \(\bold{T}\) と \(\bold{N}\) が決まったところで、 従法線ベクトル \(\bold{B}\) を次のベクトル積で定義します。

\[ \bold{B} = \bold{T} \times \bold{N} \]

従法線は Binormal なので、記号は \(\bold{B}\) または \(\bold{b}\) です。

ベクトル積の大きさは、二つのベクトルのはる平行四辺形の面積です。この場合はベクトル積をなすのが \(| \bold{T} | = 1\) と \(| \bold{N} | = 1\) で、それらが直行しているわけですから、 \(\bold{T}\) と \(\bold{N}\) とがつくる正方形の面積が \(\bold{B}\) の大きさになり、 \(| \bold{B} | = 1\) になります。

\(\bold{B}\)、\(\bold{T}\)、\(\bold{N}\) の関係と覚え方

さらに、三つのベクトルの直交関係から次の式もなりたちます。

\[ \begin{aligned} \bold{T} &= \bold{N} \times \bold{B}\\ \bold{N} &= \bold{B} \times \bold{T} \end{aligned} \]

上の図から明らかですが、パッパッと書くには次のような覚え方もあります。\(\bold{B}\) (ボ)、\(\bold{T}\) (タ)、\(\bold{N}\) (ン) の順番に三角形を書いて、時計回りに矢印を書きます。

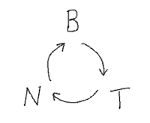
そして例えば \(\bold{B}\) を \(\bold{T}\) と \(\bold{N}\) で書きたいなら、時計回りにベクトル積を作ります。

さらに、ベクトル積は掛け算の順番を変えると符号が変わりますので、次の関係にも書けます。

\[ \begin{aligned} - \bold{B} &= \bold{N} \times \bold{T}\\ - \bold{T} &= \bold{B} \times \bold{N}\\ - \bold{N} &= \bold{T} \times \bold{B} \end{aligned} \]

三つのベクトルについては以上です。

平面の名称

さて、もう一度上の図をみてください。

上で「曲線が局所的に乗っている平面を接触平面である」といいましたが、さらにあと二つ名前がついてます。

\(\bold{N}\) と \(\bold{B}\) がはる平面は 法平面 といいます。これは接線に垂直な平面になります。また \(\bold{B}\) と \(\bold{T}\) がはる平面は 展直平面 (Rectifying plane) といいます。

以上、新しい名前がたくさん出てきましたが、接触平面をスタート地点にして順番に考えていけば、特に難しいことはありませんね。