ストークスの定理 問題 (1)
\(\overrightarrow{F} = -y^2 \overrightarrow{i} + x \overrightarrow{j} + z^2 \overrightarrow{k}\) のベクトル場で、閉曲線 \(C\) に沿う線積分を求めよ。 ただし、 \(C\) は平面 \(y+z=2\) と \(x^2+y^2=1\) の交線とする。
問題は、線積分を求めよ、という問題です。
\[\int_C \overrightarrow{F} \cdot d\overrightarrow{r}\]
積分経路となる閉曲線 \(C\) は少々厄介なところにあるので、線積分をそのまま計算するのは大変です。
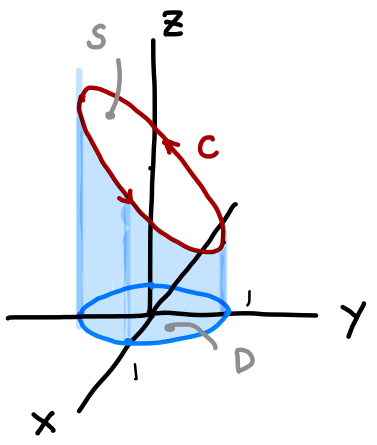
そこで、ストークスの定理を使って \(S\) での面積分に置き換えましょう。すると、\(S\) の法線ベクトルは簡単にわかりますし、 そこからさらに \(S\) の \(xy\) 平面への正射影 \(D\) に変換すると、\(D\) は単純な単位円なので計算も楽にいけそうですね。
ストークスの定理で面積分に
ここでは、線積分をこのまま計算するのではなく、ストークスの定理で面積分に置き換えて計算してみましょう。
閉曲線 \(C\) によって囲まれる面を \(S\) とすると、ストークスの定理から求める線積分は次の面積分に等しいことがわかります。
\[ \int_C \overrightarrow{F} \cdot d\overrightarrow{r} = \int_S (\nabla \times \overrightarrow{F}) \cdot \overrightarrow{n} dS \]
ちなみに \(\overrightarrow{n} dS\) は面積ベクトルで、\(d\overrightarrow{S}\) としても同じことです。
\(\nabla \times \overrightarrow{F}\) を求める
まず、\(\nabla \times \overrightarrow{F}\) は次の計算で求まります。
法線ベクトルは?
さて、法線ベクトル \(\overrightarrow{n}\) はどうなるでしょうか。
平面の式からただちにわかる
1つの方法としては、一般に平面 \(Ax + By + Cz + D = 0\) の時、単位法線ベクトルは、
\[ \overrightarrow{n} = \frac{A \overrightarrow{i} + B\overrightarrow{j} + C \overrightarrow{k}}{\sqrt{A^2 + B^2 + C^2}} \]
です。
平面の法線ベクトルが上の式でもとまることについては「空間での法線と法線ベクトル」をみてください。
ここでは \(A = 0, B=1, C=1, D=-1\) の場合なので
\[ \overrightarrow{n} = \frac{\overrightarrow{j} + \overrightarrow{k}}{\sqrt{2}} \]
であることがわかります。
勾配が等位面に垂直であることから求める
今回は \(S\) が平面であることがわかっているので、法線ベクトルは簡単に求まりました。 しかし、もし \(S\) が曲面なら上の方法は使えません。多くの場合に適用できるように、もうひとつ別の求め方をみておきましょう。
曲面 \(S\) が \(z = g(x,y)\) で与えられている時、これは \(f(x,y,z) = z - g(x, y) = 0\) なる等位面を表しているとみることができます。 勾配 (ベクトル) \(\nabla f\) は等位面に垂直になりますから、単位法線ベクトル \(\overrightarrow{n}\) は、次の式で求まります。
勾配が等位面に垂直である点については「f の勾配が等位面に垂直であるのはなぜか」も参考にしてください。
ここで、\(\nabla f\) は次式です。
\[ \begin{aligned} \nabla f &= \frac{\partial f}{\partial x} \overrightarrow{i} + \frac{\partial f}{\partial y} \overrightarrow{j} + \frac{\partial f}{\partial z} \overrightarrow{k}\\ &= - \frac{\partial g}{\partial x} \overrightarrow{i} - \frac{\partial g}{\partial y} \overrightarrow{j} + \overrightarrow{k}\\ \end{aligned} \]
また、\(\nabla f\) のノルム (大きさ) は次の式でもとまります。
\[ \| \nabla f \| = \sqrt{\Big( \frac{\partial g}{\partial x} \Big)^2 + \Big( \frac{\partial g}{\partial y} \Big)^2 + 1} \]
さて、この問題では \(S\) がのっている面は \(y+z=2\) ですから、 \(z = 2 - y = g(x, y)\) とおきます。(\(x\) は含まれていませんが、一応この形で書いておきます)
\[ \frac{\partial g}{\partial x} = 0, \ \frac{\partial g}{\partial y} = -1 \]
よって、\(\nabla f = \overrightarrow{j} + \overrightarrow{k}\)、\(\| \nabla f \| = \sqrt{2} \) なので法線ベクトルは次式になります。
\[ \overrightarrow{n} = \frac{\overrightarrow{j} + \overrightarrow{k}}{\sqrt{2}} \]
当然ながら、平面の法線ベクトルとして直ちに求めたベクトルと同じですね。
ここまでで、\(\overrightarrow{F}\) の回転 \(\nabla \times \overrightarrow{F}\) と \(\overrightarrow{n}\) が求まりました。
ストークスの定理の面積分の部分、
\[ \int_S (\nabla \times \overrightarrow{F}) \cdot \overrightarrow{n} dS \]
求めるので、これらの内積を計算しましょう。
内積 \((\nabla \times \overrightarrow{F}) \cdot \overrightarrow{n}\) の計算
ベクトルの内積は \(x, y, z\) 成分をそれぞれ掛け算して足し合わせるのでしたね。成分を計算しやすいように、 \(\langle x, y, z \rangle\) の形でベクトルの成分表示をして計算します。
面積分の計算
計算の材料が揃ってきたので、面積分の計算をしていきます。
\(S\) の \(xy\) 平面への正射影 \(D\) を考えると
\[ \begin{aligned} dS &= \sqrt{\Big( \frac{\partial g}{\partial x} \Big)^2 + \Big( \frac{\partial g}{\partial y} \Big)^2 + 1} dxdy\\ &= \sqrt{2} dxdy \end{aligned} \]
\[ \begin{aligned} \int_S (\nabla \times \overrightarrow{F}) \cdot \overrightarrow{n} dS &= \int_S \frac{2y + 1}{\sqrt{2}} dS\\ &= \int_D \frac{2y + 1}{\sqrt{2}} \sqrt{2} dxdy\\ &= \int_D 2y + 1 dxdy \end{aligned} \]

ここで \(D\) は原点を中心とする半径 \(1\) の円だから、極座標に変換して計算すると、 \(x = \rho \cos \theta, y = \rho \sin \theta, 0 \le \rho \le 1, 0 \le \theta \le 2\pi, dxdy = \rho d\rho d\theta \) から
\[ \begin{aligned} \int_D 2y + 1 dxdy &= \int_0^{2\pi} \int_0^1 (2 \rho \sin \theta + 1) \rho d\rho d\theta\\ &= \int_0^{2\pi} \Big[ \frac{2}{3} \rho^3 \sin \theta + \frac{\rho^2}{2} \Big]_0^1 d\theta\\ &= \int_0^{2\pi} \Big(\frac{2}{3}\sin \theta + \frac{1}{2}\Big) d\theta\\ &= \Big[ \frac{2}{3}(-\cos \theta) + \frac{\theta}{2} \Big]_0^{2\pi} \\ &= \frac{1}{2}(2\pi - 0)\\ &= \pi \end{aligned} \]
これが求める答えになります。