スカラー場の勾配 問題 (1)

$\nabla$ は勾配ベクトル の演算子で、次のように定義されます。

スカラー関数に作用して、そのスカラー関数の勾配ベクトルを求めます。

$r$ は原点からの距離を表す関数で、$r = \sqrt{x^2 + y^2 + z^2}$ です。

$r$ を $x$、$y$、$z$ それぞれで偏微分すると、次のようになります。

$$\begin{aligned} \frac{\partial r}{\partial x} &= \frac{1}{2} (x^2+y^2+z^2)^{-\frac{1}{2}} \cdot 2x\\ &= \frac{x}{\sqrt{x^2+y^2+z^2}}\\ &= \frac{x}{r} \end{aligned}$$

$y$、$z$ に対しても同様に計算して、$\cfrac{\partial r}{\partial y} = \cfrac{y}{r}$、 $\cfrac{\partial r}{\partial z} = \cfrac{z}{r}$ となります。

ゆえに、$r$ の勾配ベクトルは次のようになります。

$$\begin{aligned} \nabla r &= \frac{\partial r}{\partial x} \overrightarrow{i} + \frac{\partial r}{\partial y} \overrightarrow{j} + \frac{\partial r}{\partial z} \overrightarrow{k} \\ &= \frac{x}{r} \overrightarrow{i} + \frac{y}{r} \overrightarrow{j} + \frac{z}{r} \overrightarrow{k}\\ &= \frac{x \overrightarrow{i} + y \overrightarrow{j} + z \overrightarrow{k}}{r}\\ &= \frac{\overrightarrow{r}}{r} \end{aligned}$$

よって、答えは(D) です。

$\nabla r = \cfrac{\overrightarrow{r}}{r}$ の意味は？

この問題文の関係、つまり $\nabla r = \cfrac{\overrightarrow{r}}{r}$ はどういうことか、少し考えてみましょう。

まず、$\overrightarrow{r} = x \overrightarrow{i} + y \overrightarrow{j} + z \overrightarrow{k}$ は、 次のグラフのように原点から放射状、外向きに向かうベクトル場を作ります。

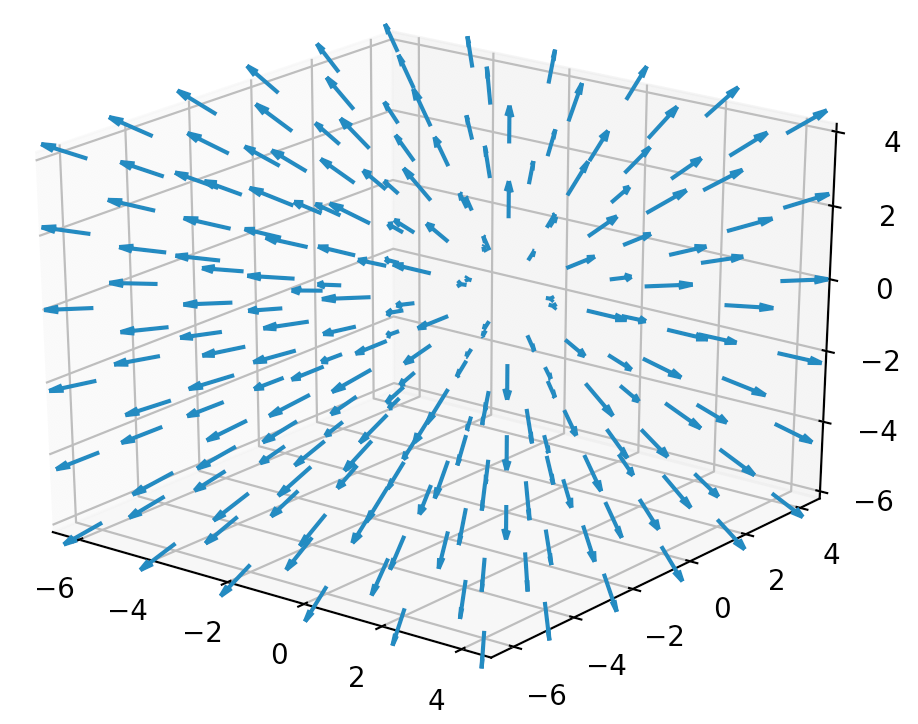
ベクトル $\overrightarrow{r}$ の大きさは、原点からの距離に比例して大きくなります。

$\cfrac{\overrightarrow{r}}{r} = \cfrac{\overrightarrow{r}}{| \overrightarrow{r} | }$ というベクトルは、 ベクトル $\overrightarrow{r}$ 向きの単位ベクトル (大きさ 1 のベクトル) を表します。

さて、この問題で勾配ベクトルをとるスカラー関数は、原点からの距離を表す関数 $r(x,y,z) = \sqrt{x^2 + y^2 + z^2}$ ですから、 等位面は球面になります。

勾配ベクトルは等位面に対して垂直方向を向き、そのスカラー関数の値を最も増加させる向きを示します。

つまり $\nabla r = \cfrac{\overrightarrow{r}}{r}$ という結果は、 『空間上の点 A から、どの方向に動いたら最も効率よく $r$ が増えるか ($r$ の勾配が急であるか) 』 というと、それは 『半径方向に動いた時であり、そのときの増加割合は 1 である』 ということを意味しています。

「増加割合は1である」というところは、半径方向に 1 動いたら、半径が 1 増加する、ということですから、当然のことですね。

この状況を理解していれば $\nabla r = \cfrac{\overrightarrow{r}}{r}$ という関係は、とても自然な結論であることがよくわかると思います。