複素形フーリエ級数 例題(3)

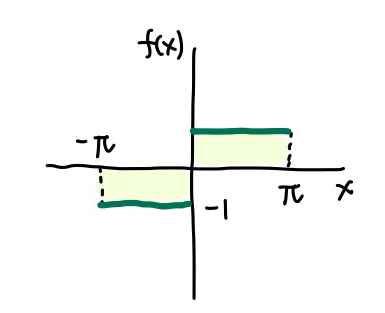
\([-\pi, \pi]\) で定義された関数 \(f(x)\) の複素形フーリエ級数は、次の式で表されます。

\[ \begin{aligned} f(x) &= \sum_{n = -\infty}^{\infty} c_n e^{inx}\\ c_n &= \frac{1}{2\pi}\int_{-\pi}^{\pi} f(x) e^{-inx} dx \end{aligned} \]

このフーリエ係数 \(c_n\) を計算すれば、求める級数がわかります。

まず、\(n=0\) のとき

\[ \begin{aligned} c_0 &= \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) dx\\ &= \frac{1}{2\pi}\Big\{ \int_{-\pi}^{0} (-1) dx + \int_0^{\pi} dx \Big\}\\ &= 0 \end{aligned} \]

です。\(f(x)\) が奇関数であることに気付いていれば、計算するまでもなく \(c_0 = 0\) であることはわかりますね。

\(n \ne 0\) のときは

\[ \begin{aligned} c_n &= \frac{1}{2\pi} \Big\{ \int_{-\pi}^0 -e^{-inx} dx + \int_{0}^{\pi} e^{inx} dx \Big\}\\[1.4em] &= \frac{1}{2\pi} \Big\{ \Big[ \frac{1}{in} e^{-inx} \Big]_{-\pi}^{0} + \Big[ -\frac{1}{in} e^{-inx} \Big]_0^{\pi} \Big\}\\[1.4em] &= \frac{1}{2\pi} \Big\{ \frac{1}{in}(1-e^{in\pi}) - \frac{1}{in}(e^{-in\pi} -1) \Big\}\\[1.4em] &= \frac{1}{2\pi} \frac{1}{in} (1-e^{in\pi} -e^{-in\pi} + 1)\\[1.4em] &= \frac{1}{2\pi ni} \{ 2 - (e^{in\pi} + e^{-in\pi})\}\\[1.4em] &= \frac{1}{2\pi ni} (2 - 2 \cos n\pi)\\[1.4em] &= \frac{1}{2\pi ni} \{2 - 2 (-1)^n\}\\[1.4em] &= \frac{1-(-1)^n}{\pi ni}\\[1.4em] &= -\frac{1-(-1)^n}{\pi n} i \end{aligned} \]

となります。

ここで、\(n\) が偶数の時、分子の \(1-(-1)^n = 0\) であるため \(c_n = 0\)。 奇数の時は \(1-(-1)^n = 2\) であることに注意して整理すると \(c_n\) は

\[ c_n = -\frac{2}{\pi(2n+1)} i \]

と書けます。

したがって、問題の関数 \(f(x)\) の複素形フーリエ級数は次のようになります。

\[ c_n = -\frac{2}{\pi} i \sum_{n=-\infty}^{\infty} \frac{1}{2n+1} e^{i(2n+1)x} \]

• 複素形フーリエ級数 例題(1)
• 複素形フーリエ級数 例題(2)
• 複素形フーリエ級数 例題(3)