フーリエ余弦級数 例題(1)

\(f(x)\) をフーリエ「余弦」級数に展開するためには、\(f(x)\) を偶関数とみる必要があります。

問題では \(x\) が \(0 \lt x \lt L\) で定義されていますが、この関数を偶周期的に次のように \(-L \lt x \lt 0\) に拡張して考えることにします。

これで、\(f(x)\) が偶関数になりました。

そこで、フーリエ余弦級数を計算します。

\(n=0\) のとき

\[ \begin{aligned} a_0 &= \frac{2}{L} \int_0^L x dx\\ &= \frac{2}{L} \Big[\frac{x^2}{2}\Big]_0^L\\ &= \frac{2}{L} \frac{L^2}{2}\\ &= L \end{aligned} \]

\(n = 1, 2, \cdots\) のとき

\[ \begin{aligned} a_n &= \frac{2}{L} \int_0^L x \cos\frac{n\pi x}{L} dx\\[1.4em] &= \frac{2}{L} \Big\{ \Big[ \frac{L}{n\pi} x \sin\frac{n\pi x}{L} \Big]_0^L - \int_0^L \frac{L}{n\pi}\sin\frac{n\pi x}{L}dx \Big\}\\[1.4em] &= \frac{2}{L} \Big\{ -\frac{L}{n\pi} \int_0^L \sin\frac{n\pi x}{L}dx \Big\}\\[1.4em] &= -\frac{2}{n\pi} \Big[ -frac{L}{n\pi} \cos\frac{n\pi x}{L} \Big]_0^L\\[1.4em] &= \frac{2L}{n^2\pi^2}(\cos n\pi - 1)\\[1.4em] &= \frac{2L}{n^2\pi^2}\{(-1)^n - 1\} \end{aligned} \]

したがって、フーリエ余弦級数は次のようになります。

\[ \begin{aligned} f(x) &= \frac{a_0}{2} + \sum_{n=1}^{\infty} a_n\cos\frac{n\pi x}{L}\\ &= \frac{L}{2} + \sum_{n=1}^{\infty} \frac{2L}{n^2\pi^2}\{(-1)^n - 1\}\cos\frac{n\pi x}{L} \end{aligned} \]

この級数の始めの数項を書き下すと、次のようになります。

\[ f(x) = \frac{L}{2} - \frac{4L}{\pi^2}\Big(\cos\frac{\pi x}{L} + \frac{1}{9}\cos\frac{3\pi x}{L} + \frac{1}{25}\cos\frac{5\pi x}{L} + \cdots \Big) \]

\(L = \pi\) として、このグラフを描くと、次のようになりました。

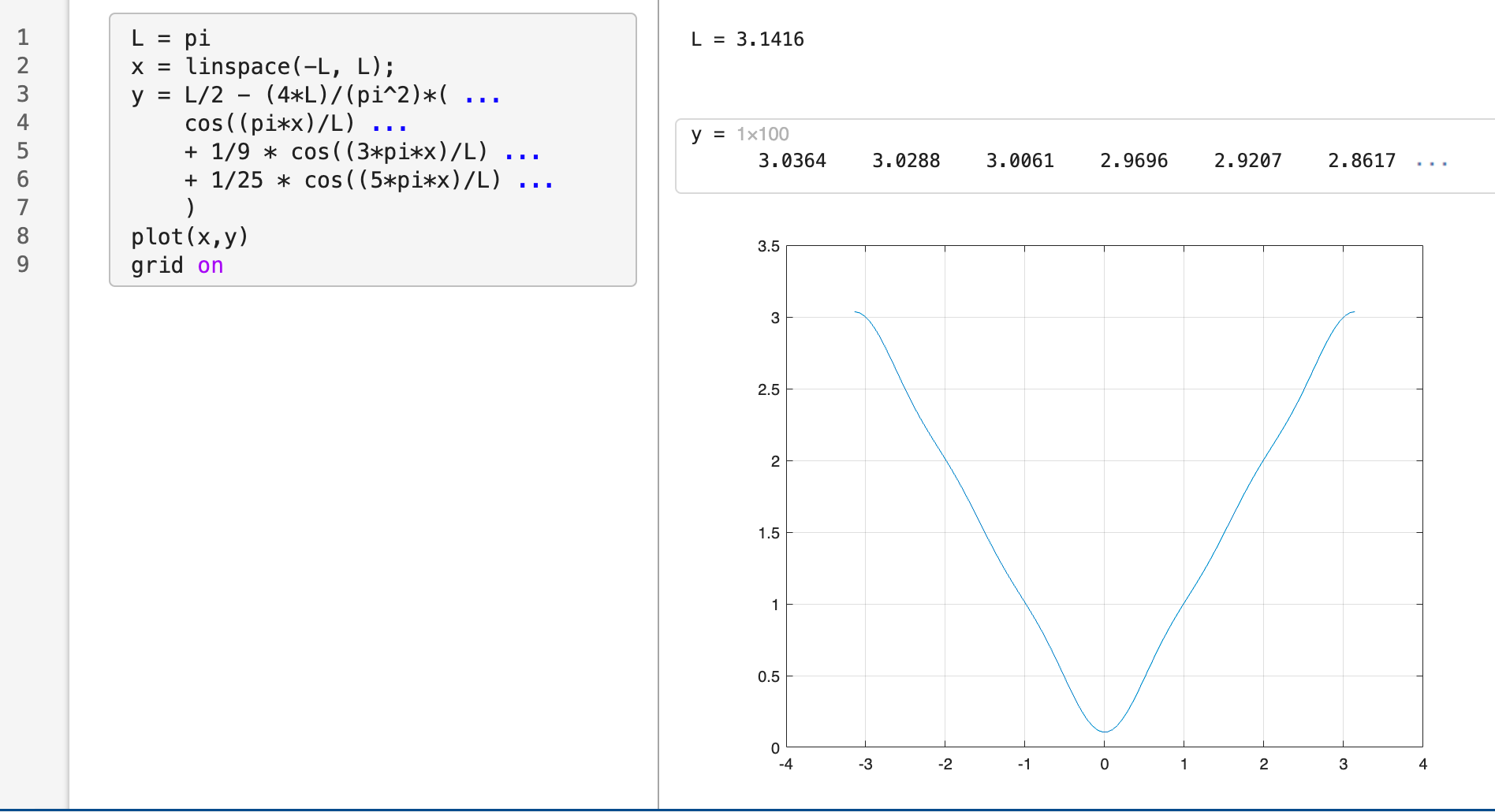
\(n=5\) の項まででも、確かに、想定した通りのグラフに近い形になっていることがわかりますね。

• フーリエ余弦級数 例題(1)
• フーリエ余弦級数 例題(2)