フーリエ正弦積分 例題(2)
次の関数のフーリエ正弦積分を求めよ。
\[ f(x) = \begin{cases} \ \ x \ \ &(0 \lt x \lt 1)\\ \ \ 0 \ \ &(x \gt 1) \end{cases} \]
\(f(x)\) を奇周期的に拡張して奇関数とみなすことで、フーリエ正弦積分の式にあてはめることができます。
フーリエ正弦積分は
\[ \begin{aligned} f(x) &= \int_0^{\infty} B(s) \sin sx ds\\ B(s) &= \frac{2}{\pi} \int_{0}^{\infty} f(t) \sin st dt\\ \end{aligned} \]
ですから、この問題の場合は、
\[ \begin{aligned} B(s) &= \frac{2}{\pi} \int_0^1 t \sin st dt\\[1.4em] &= \frac{2}{\pi} \Big\{ \Big[ -\frac{t \cos st}{s} \Big]_0^1 - \int_0^1 -\frac{\cos st}{s} dt \Big\}\\[1.4em] &= \frac{2}{\pi} \Big( -\frac{\cos s}{s} + \frac{1}{s} \int_0^1 \cos st dt \Big)\\[1.4em] &= \frac{2}{\pi} \Big( -\frac{\cos s}{s} + \frac{1}{s} \Big[ \frac{\sin st}{s} \Big]_0^1 \Big)\\[1.4em] &= \frac{2}{\pi} \cdot \frac{\sin s - s \cos s}{s^2} \end{aligned} \]
となります。
したがって、\(f(x)\) のフーリエ正弦積分表示は
\[ f(x) = \frac{2}{\pi} \int_0^{\infty} \frac{\sin s - s \cos s}{s^2} \sin xs ds \]
となります。
尚、奇周期的に拡張したので、\(f(x)\) は次のような関数とみなしたということになります。
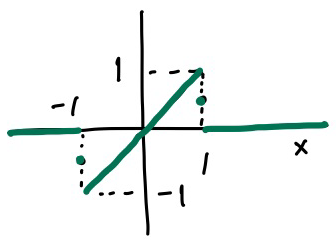
また、フーリエ積分は不連続点で、右側極限値と左側極限値の平均値をとりますので、この積分は不連続点 \(x=1\) で \(1/2\) に、 \(x=-1\) で \(-1/2\) に収束します。
したがって、
\[ \begin{aligned} \frac{2}{\pi} \int_0^{\infty} \frac{\sin s - s \cos s}{s^2} \sin xs ds = \begin{cases} \ \ 0 \ \ &(|x| > 1)\\[1.2em] \ \ \cfrac{1}{2} \ \ &(x = 1)\\[1.2em] \ \ x \ \ &(|x| < 1)\\[1.2em] \ \ -\cfrac{1}{2} \ \ &(x = -1) \end{cases} \end{aligned} \]
となります。積分の値に注目すると、次のようになります。
\[ \begin{aligned} \int_0^{\infty} \frac{\sin s - s \cos s}{s^2} \sin xs ds = \begin{cases} \ \ 0 \ \ &(|x| > 1)\\[1.2em] \ \ \cfrac{\pi}{4} \ \ &(x = 1)\\[1.2em] \ \ \cfrac{\pi x}{2} \ \ &(|x| < 1)\\[1.2em] \ \ -\cfrac{1}{4} \ \ &(x = -1) \end{cases} \end{aligned} \]
- フーリエ正弦積分 例題(1)
- フーリエ正弦積分 例題(2)