弧長の求め方 - パラメータ表示
ここでも引き続き弧長の計算方法を考えましょう。
前回は平面の直交座標系 \(xy\) 平面での弧の長さを考えました。
今回も同じく \(xy\) 平面ではありますが、\(x\) と \(y\) が \(t\) をパラメータを使って \(x = f(t)\)、\(y = g(t)\) という形で記述されている場合に弧長がどのように表されるか考えましょう。 \(t\) の範囲は \([a, b]\) とします。
この範囲で \(f\)、\(g\) は微分可能、つまり曲線が滑らかにつながっているとします。
具体的なイメージとしては、\(x = 2 \cos t\)、\(y = 2 \sin t\) で \(t\) の範囲が \([0, \pi]\) という感じです。
これは半径 \(2\) の円の上半分ですね。二乗すると \( x^2 = 4 \cos^2 t\)、\(y^2 = 4 \sin^2 t\) ですから、 \(x^2 + y^2 = 4 (\cos^2 t + \sin^2 t) = 4\) です。
前回同様、弧の長さを考えるには考えている区間の弧を \(n\) 個に分けて考え、微小な区間では直線に近似して考えることができるので、それを足し合わせて弧長を求める方針です。
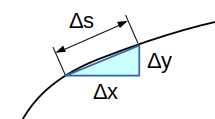
ポイントは次のように、\(\Delta t\) が出てくるように式変形するところです。
\[ \begin{aligned} \Delta s_k &= \sqrt{ (\Delta x)^2 + (\Delta y)^2}\\ &= \sqrt{ \Big( \frac{\Delta x}{\Delta t} \Big)^2 + \Big( \frac{\Delta y}{\Delta t} \Big)^2 } \Delta t \end{aligned} \]
したがって、\([a, b]\) での弧長 \(L\) は