弧長の求め方 (極座標表示) の例題 (2) カージオイド

\(r = a( 1 - \cos \theta )\) の弧長を求めよ。(\(a\) は正の定数)

問題の曲線はカージオイド (cardioid) になります。カージオイドは心臓型ともいわれます。

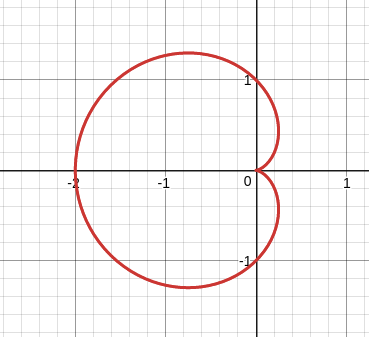
一般に \( r = a \pm b \cos \theta\) で \(a/b = 1\) のときはカージオイドになります。

問題のカージオイドは \(r = a(1-\cos \theta)\) ですが、この中のマイナスをプラスに変えて、 \(r = a(1+\cos \theta)\) にしてもやはりカージオイドです。図形の向きが変わります。

極座標で \(x = r(\theta) \cos \theta\)、\(y = r(\theta) \sin \theta\) で \(\theta\) の範囲を \( [\alpha, \beta] \) としたときの弧長 \(L\) は次の式で求められます。

\[ \begin{aligned} L &= \int_{\alpha}^{\beta} \sqrt{ r^2 + \Big(\frac{dr}{d\theta}\Big)^2 } d\theta \end{aligned} \]

なぜこの式で弧長がわかるか、ということについては「弧長を求める - 極座標表示」をみてください。

さて、それではこの公式を使って、問題を解きましょう。

問題のカージオイドは上の図のように \(x\) 軸に対し対称なので、\(x\) 軸を境に上側 (\(y \ge 0\)) の弧長を \(L_1\) とすると、全体の弧長 \(L\) は \(L = 2L_1\) です。

\(L_1\) はカージオイドの \(0 \le \theta \le \pi \) の範囲ですから、\(L\) は次の式で求まります。

\[ \begin{aligned} L &= 2L_1\\ &= 2 \int_{0}^{\pi} \sqrt{r^2 + \Big(\frac{dr}{d\theta} \Big)^2} d\theta \end{aligned} \]

あとは、この積分を計算すれば良いだけです。

ルートの中身が一見ややこしいので簡単にしましょう。

\(r\) は問題文で \(r = a(1-\cos \theta)\) として与えられていますから、これを \(\theta\) で微分すると、 \(\displaystyle\frac{dr}{d\theta} = a \sin \theta\) です。

よって、上の式のルートの中身は次のようになります。

\[ \begin{aligned} r^2 + \Big(\frac{dr}{d\theta}\Big)^2 &= a^2 (1 - \cos \theta)^2 + (a \sin \theta)^2\\ &= a^2 (1 - 2\cos \theta + \cos^2 \theta + \sin^2 \theta)\\ &= a^2 (1 - 2\cos \theta + 1)\\ &= 2a^2 (1-\cos \theta) \end{aligned} \]

これがルートの中身であることを考えると、\((1-\cos \theta) \) の部分も、何かの二乗の形になっていたら、ルートをはずせてありがたいので、もう少し式変形しましょう。

\[ \begin{aligned} \cos \theta &= \cos 2 \frac{\theta}{2}\\ &= \cos^2 \frac{\theta}{2} - \sin^2 \frac{\theta}{2}\\ &= 1 - 2 \sin^2 \frac{\theta}{2}\\ \therefore \ 1 - \cos \theta &= 2 \sin^2 \frac{\theta}{2} \end{aligned} \]

よって、ルートの中身は次のようになります。

\[ \begin{aligned} r^2 + \Big(\frac{dr}{d\theta}\Big)^2 &= 2a^2 \cdot 2 \sin^2 \frac{\theta}{2}\\ &= 4a^2 \sin^2 \frac{\theta}{2} \end{aligned} \]

ここで、一般に \(\sqrt{x^2} = |x|\) であることに注意すると、

\[ \begin{aligned} \sqrt{4a^2 \sin^2 \frac{\theta}{2}} &= \Big| 2a \sin \frac{\theta}{2} \Big| \end{aligned} \]

です。ここで、\(0 \le \theta \le \pi\) の範囲で \(\sin \displaystyle\frac{\theta}{2} \ge 0\) ですから、絶対値記号はそのままはずすことができます。この点に注意して、次の式変形をみてください。

以上から、弧長 \(L\) は次のように計算できます。

\[ \begin{aligned} L &= 2L_1\\ &= 2 \int_{0}^{\pi} \sqrt{r^2 + \Big(\frac{dr}{d\theta} \Big)^2} d\theta\\ &= 2 \int_{0}^{\pi} \sqrt{4a^2 \sin^2 \frac{\theta}{2}} d\theta\\ &= 2 \int_{0}^{\pi} \Big| 2a \sin \frac{\theta}{2} \Big| d\theta\\ &= 4a \int_{0}^{\pi} \sin \frac{\theta}{2} d\theta\\ &= 4a \Big[-2 \cos \frac{\theta}{2}\Big]_{0}^{\pi}\\ &= -8a (0 - 1)\\ &= 8a \end{aligned} \]

以上から求める弧長 \(L\) は \(L = 8a\) であることがわかりました。