曲率と曲率半径 例題 (1): 円の曲率
半径 \(a\) の円の曲率を求めよ。
答えは定義から簡単に出せます。
曲率 \(\kappa\) は曲率半径 \(\rho\) と、\(\kappa = \displaystyle\frac{1}{\rho}\) の関係にあって、 ここでは半径 \(a\) の円なので \(\rho = a\)。したがって、曲率は \(\kappa = \displaystyle\frac{1}{a}\) である。
という風に即答のところですが、地味に習ったことを駆使して「計算」してみて、本当にそうなるかみておきましょう、というのがこの問題の狙いです。
定義から曲率は次の式で与えられます。
ここで、\(\overrightarrow{t}\) は単位接線ベクトルです。
単位接線ベクトル \(\overrightarrow{t}\) は、弧長 \(s\)でパラメータ表示した位置ベクトル \(\overrightarrow{r}(s)\) を用いて、次で得られます。
「空間曲線の単位接線ベクトル」をみてください。
したがって、曲率は次の式で求まります。
さて、問題は半径 \(a\) の円を考えています。
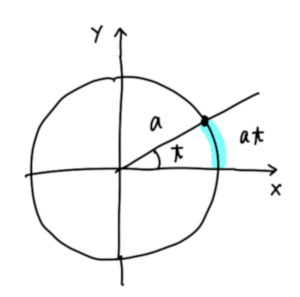
原点\(O\) を中心とした、半径 \(a\) の円上の点\(P\) の位置ベクトル\(\overrightarrow{r}\)は、\(OP\) が\(x\) 軸となす角\(t\) を用いて、 次のように書けます。
\[\overrightarrow{r}(t) = a \cos t \overrightarrow{i} + a \sin t \overrightarrow{j}\]
弧長 \(s\) (図の水色の部分) は、\(s = a \cdot t\)。つまり \(t = \displaystyle\frac{s}{a}\) ですから、上の式を書き換えると次になります。
\[\overrightarrow{r}(s) = a \cos \frac{s}{a} \overrightarrow{i} + a \sin \frac{s}{a} \overrightarrow{j}\]
曲線上の位置ベクトルが弧長\(s\)をパラメータに書くことができました。上で見たようにこれの二階微分したベクトルの大きさが曲率となります。
\[ \begin{aligned} \overrightarrow{t} &= \overrightarrow{r}'(s)\\ &= - \sin \frac{s}{a} \overrightarrow{i} + \cos \frac{s}{a} \overrightarrow{j} \end{aligned} \]
もう一度 \(s\) で微分すると
\[ \overrightarrow{r}''(s) = - \frac{1}{a} \cos \frac{s}{a} \overrightarrow{i} - \frac{1}{a} \sin \frac{s}{a} \overrightarrow{j} \]
この大きさが曲率 \(\kappa\) となるはずなので、計算すると次の通り。
\[ \begin{aligned} \kappa &= | \overrightarrow{r}''(s) |\\ &= \sqrt{\Big(-\frac{1}{a} \cos \frac{s}{a}\Big)^2 + \Big(-\frac{1}{a} \sin \frac{s}{a} \Big)^2 } \\ &= \sqrt{\frac{1}{a^2} \Big( \cos^2 \frac{s}{a} + \sin^2 \frac{s}{a} \Big)} \\ &= \frac{1}{a} \end{aligned} \]
以上から、確かに曲率は \(\displaystyle\frac{1}{a}\) になりました。